Вторым, дополняющим его уравнением является уравнение баланса вещества. Через поперечное сечение выделенного слоя с единичной площадью за единицу времени проходит объем воды, равный скорости фильтрования. Следовательно, массовое количество вещества задерживаемого слоем, равно

( 2.6)

Извлекаемые слоем из воды частицы образуют осадок на зернах слоя, накапливающийся в ходе процесса. Количество отложений в слое толщиной Δx; составляет ρ*Δх, а скорость накопления отложений в слое или количество вещества, накапливающегося в нем за единицу времени t, равно

(12.7)

Приравнивая выражения (12.6) и (12.7), получим

'

Дифференциальное уравнение (12.8) является уравнением баланса веществ. Оно показывает, что количество вещества, извлеченного слоем Ах из воды за единицу времени, равно количеству накопившегося в этом слое вещества за тот же промежуток времени.

Дифференцируя уравнение (12.5) по времени и учитывая уравнение баланса (12.8), получим

(12.9)

Это уравнение в дифференциальной форме описывает кинетику процесса осветления при фильтровании суспензий. Аналогично уравнению (12.9) получим дифференциальное уравнение для плотности насыщения

(12.10)

описывающее в дифференциальной форме процесс изменения плотности насыщения фильтрующей загрузки осадком по ее высоте с течением времени. Выражения (12.9) и (12.10) интегрируются, но решение получается в виде бесконечного ряда и его трудно использовать для практических расчетов, которые упрощаются, если воспользоваться критериями подобия для процесса осветления, получаемыми из анализа дифференциального уравнения (12.9). С этой целью преобразуем уравнение (12.9), введя безразмерное отношение мгновенной концентрации к начальной концентрации частиц в воде, поступающей на фильтр: У=С/С0. Тогда

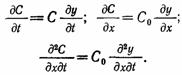
Подставляя эти значения в уравнение (12.9) и сокращая по- сТОянный множитель С0, получим

(12.11)

Введем теперь новые независимые безразмерные переменные

X = bx, Т = at(12.12)

Подставляя эти значения в уравнение (12.11) и сокращая постоянные множители а и b, получим

(12.13)

В уравнение (12.13) в отличие от исходного уравнения (12.9) непосредственно не входят параметры фильтрования а и Ь, которые характеризуют формы протекания процесса. Следовательно, оно является общим для всего многообразия условий протекания процесса фильтрования.

Безразмерные переменные X и Т устанавливают подобие протекания процесса осветления при разных условиях и являются критериями подобия. Изменение концентрации взвеси в воде при ее движении через зернистый слой определяется только значением этих критериев, т. е.