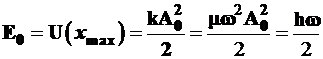, (3.114)

откуда 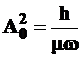и 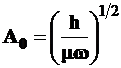. (3.115)

Формулы (3.112) и (3.115) практически дают один и тот же результат, поскольку классическая амплитуда А0

– это максимальное отклонение осциллятора от положения равновесия, тогда как квадратичная “амплитуда” усреднена по всем положениям осциллятора, а понятие точной траектории и предельного отклонения не имеет смысла в квантовой механике.

Можно показать, что соответствие классической амплитуды и квантово-механического среднеквадратичного отклонения сохраняется и в других состояниях осциллятора, а именно:

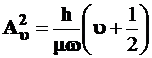и 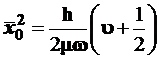(3.120)

(в квазиклассическом подходе) (в квантовомеханическом подходе)

3.5.18.

Среднеквадратичные амплитуды играют важную роль в экспериментах, связанных с определением равновесных положений ядер в молекулах, например, в электронографии или в рентгеноструктурном анализе. Они также позволяют на основе опытных колебательных спектров (инфракрасного поглощения и комбинационного рассеяния) определить пределы изменения молекулярных “размеров” за счет колебательных деформаций ядерного остова молекулы.

3.6. Сравнение свойств “ящика”, “ротатора” и осциллятора.

3.6.1.

Три рассмотренные модели простейших одномерных движений в ограниченном пространстве позволяют проследить некоторые общие качественные закономерности, касающиеся состояний и уровней квантово-механических систем. Они наглядно проявляются при сопоставлении энергетических диаграмм и графиков волновых функций “частицы в ящике”, “гармонического осциллятора” и “плоского ротатора”.

3.6.2.

В первом случае потенциальная энергия нулевая на выделенном интервале, и, как говорят, потенциальная “яма” имеет прямоугольную форму. Во втором случае потенциальная энергия изменяется квадратично при отклонении от равновесия и говорят о параболической форме потенциальной “ямы”. Наконец, ротатор отсутствием потенциальной энергии напоминает “ящик”. Отсюда, хотя способы нумераций уровней и отличаются, схемы квантования энергии у этих систем одинаковы – уровни расходятся с возрастанием квантового числа.

У гармонического осциллятора квантование энергии уникально – уровни эквидистантны. Благодаря этому при взаимодействии с квантами света частота поглощаемого излучения совпадает с собственной частотой молекулярного осциллятора, например, колеблющихся атомов, связанных химической связью.

Таким образом, квантование полной энергии системы определяется потенциальной функцией.

3.6.3.

В разделе 3.2.5. мы связали вырождение уровней ротатора с равноправием двух направлений вращения вокруг оси. Можно высказать еще и более общее утверждение, связывающее наличие вырождения с порядком вращательной оси системы. Плоский ротатор – это система с осью вращения бесконечного порядка. Далее будет показано, что вырожденные уровни появляются у систем, имеющих ось третьего порядка и выше.

В целом же, нам удалось приобрести некоторые необходимые навыки в решении простейших задач квантовой механики.