Табл.2.

Полиномы Эрмита и волновые функции гармонияеского

осциллятора

Читатель может сам получить формулу для нормировочных коэффициентов или взять их готовое выражение:

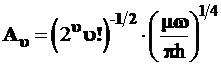. (3.108)

3.5.14.

Прямыми вычислениями нетрудно еще раз проверить свойство ортогональности волновых функций. Интегрирование по всей области возможных значений переменной хдает:

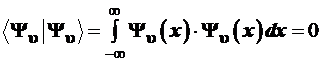, (3.109)

что наглядно видно из графиков табл. 2

Напомним, что свойство ортогональности – это общее свойство собствен-ных функций любого эрмитова оператора, к числу которых относится и гамильтониан.

3.5.15.

Все полиномы Эрмита и порождаемые ими волновые функции делятся на два класса – четные и нечетные. Ранее подобное свойство наблюдалось у волновых функций “ящика” и “ротатора”. Анализ четности волновых функций и их произведений оказывается очень полезным при оценке различных характеристик системы. Рассмотрим это на примерах.

Покажем, что среднее отклонение колеблющейся системы от положения равновесия равно нулю. Следуя 5-му постулату, запишем для υ

=0:

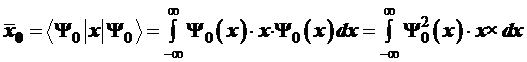. (3.110)

Подинтегральное выражение нечетное, так как образовано в виде произве-дения по правилу (чет × нечет × чет)

. Интеграл, взятый в симметричных пределах от нечетной функций, тождественно равен нулю, так что . Это же имеет место и для других состояний.

3.5.16.

Иначе обстоит дело со среднеквадратичным отклонением , на-зываемым среднеквадратичной амплитудой осциллятора. Произведем соответ-ствующие расчеты; вновь обращаясь к 5-му постулату:

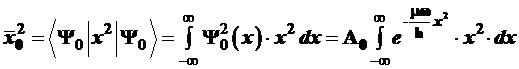, (3.111)

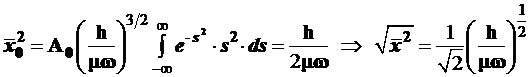(3.112)

В преобразовании (3.112) использован табличный интеграл

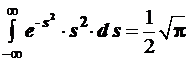. (3.113)

3.5.17.

Сравним среднеквадратичное отклонение с квадратом ампли-туды, предсказываемой на основе формулы, связывающей классическое и квантово-механическое выражение для полной энергии: