и используя подста-новки (3.74), можно упростить формулы (3.73) и (3.73а)

, (3.75)

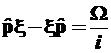, (3.76)

и для любого из дискретных уровней с номером υ

уравнение Шредингера при-обретает вид:

. (3.77)

3.5.6.

Гамильтониан (3.75) представлен в виде суммы квадратов двух операторов и , связанных коммутационным соотношением (3.76). Используя схему алгебры комплексных чисел (см. раздел 1.3.2

.), попытаемся разложить гамильтониан (3.75) на сомножители, содержащие только первые степени составляющих его операторов

, (3.78)

. (3.79)

3.5.7.

Произведения комплексных чисел коммутативны, поэтому безразличен порядок записи комплексно-сопряженных сомножителей:

(a + ib) (a - ib) = (a - ib) (a + ib) = C·C* =|C|2.

(3.80)

Так как операторы не обладают свойством коммутативности следует ожидать, что операторные произведения и различны и не равны гамильтониану, поэтому требуется исследовать их связь с гамильтонианом. При этом следует помнить, что в силу линейности операторов, слагаемые операторных сумм можно переставлять, а отдельные группы сомножителей можно объединять, так как операторные произведения обладают свойством ассоциативности.

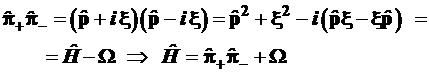, (3.81)

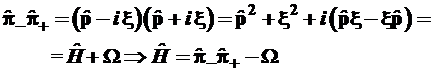. (3.82)

Таким образом, произведения операторов и отличаются от гамильтониана на постоянную величину соответственно.

Подставим найденные в (3.81) и (3.82) выражения гамильтониана в уравнение Шредингера (3.77) и перенесем постоянные множители в правую часть полученных уравнений :

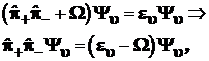(3.83)

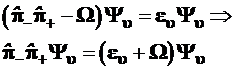(3.84)

3.5.8.

Для выяснения смысла операторов и еще раз подействуем первым из них на обе части уравнения (3.83), а вторым – на уравнение (3.84), т.е. домножим эти уравнения слева на и соответственно:

, (3.85)

. (3.86)

Подставим вместо произведений операторов () и () их выражения (3.82) и (3.81) и опять перенесем постоянные величины Ω

в правую часть уравнений:

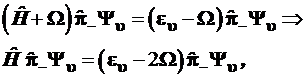(3.87)

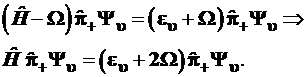. (3.88)

В итоге каждое из уравнений (3.87) и (3.88) приобрело стандартный вид уравнения Шредингера, но собственные функции в них () и () отличны от волновой функции исходного состояния Ψ