υ

, а собственные значения отличаются от исходного ευ

на постоянную

величину. Функции () отвечает уровень , на величину 2Ω сдвинутый вниз по отношению к уровню состояния Ψ

υ

, т.е. оператор произвел понижение уровня на один номер:

. (3.89)

Аналогично оператор сдвигает номер уровня и состояния Ψ

υ

на еди- ницу вверх:

. (3.90)

Функции и , полученные с помощью операторов и по формулам (3.89) и (3.90), не нормированы; но в дальнейших расчетах это несу-ественно. Состоянию отвечает уровень , а – уровень , т.е.

. (3.91)

3.5.9.

Переход к обычной энергетической шкале с использованием подста-новок (3.74б и 3.74в) дает

. (3.92)

Согласно формуле (3.92), уровни гармонического осциллятора эквидис-тантны

, и интервал между.ними равен .

3.5.10.

Продолжая исследование лесенки уровней, учтем, что сверху она неограничена, но нижняя граница определена уровнем основного состояния Ψ0

, ниже которого не существует состояний системы. Поэтому попытка подействовать оператором понижения на волновую функцию основного состояния должна дать нулевой результат, т.е. применительно к волновой функции основного уровня оператор понижения сыграет роль ее “уничтожителя” – аннигилятора:

(3.93)

Здесь целесообразно вернуться к переменной х

. С учетом выражения для (3.80) и подстановки (3.74а) формулу (3.93) после простых преобразований приводим к дифференциальному уравнению для :

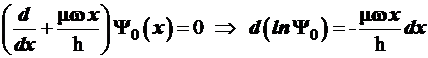, (3.94)

при интегрировании которого получим волновую функцию основного состояния:

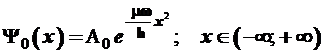. (3.95)

Далее находим нормировочный множитель А0:

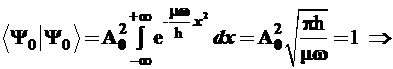(3.96)

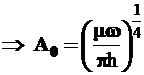. (3.97)

При раскрытии выражения (3.96) использован интеграл Пуассона:

.

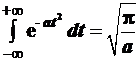3.5.11.

Волновая функция является собственной функцией гамильто-ниана. Поэтому для расчета основного уровня достаточно подействовать по-следним наи определить собственное значение

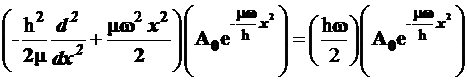(3.98)