Каждый набор отвечает одному состоянию. Все три принадлежат к одному и тому же ТРИЖДЫ ВЫРОЖДЕННОМУ уровню. Нас интересует квантовый переход [(1,1,1) Û (1,1,2); (1, 2, 1); (2,1,1)]

или в терминах дискретных квантованных уровней E111Û E112.

Примечание:

У первого уровня статистический вес (кратность вырождения) g=1,

У второго уровня статистический вес (кратность вырождения) g=3,

Статистические веса (вырожденности уровней) на энергии не сказываются.

Таким образом разность сумм квадратов квантовых чисел будет равна

[(nx) 2 + (ny) 2+ (nz) 2] возб - [(nx) 2 + (ny) 2+ (nz) 2] основн= (1+1+4) - (1+1+1) =3

Получаем формулу для энергии первого перехода (первого возбуждения) в ящике . (4.11)

Энергетические уровни электрона в атоме водорода равны:

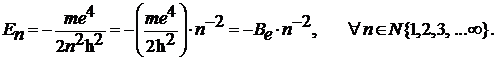(4.12)

Здесь введена энергетическая постоянная для атома H:

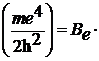(4.13)

Первый переход отвечает возбуждению (1®2) т.е. с уровня n=1 на уровень n=2.

Соответственно . (4.14)

Энергии возбуждения в ящике и в атоме равны по условию задачи.

Поэтому

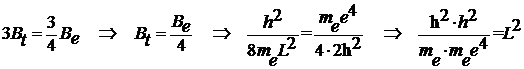. (4.15)

Вспоминаем, что боровский радиус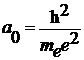

и преобразуем предыдущий результат

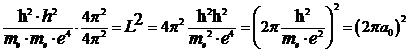. (4.16)

Откуда следует решение в аналитическом виде

L=2 p a0; (4.17)

Поскольку "диаметр" 1-й орбитали по Бору равен d0=2a0, то получается, что диаметр атома в p раз меньше размера ящика.

Этот же результат можно получить непосредственно в числовых значениях.

В данном выводе не использовались особенности системы СИ в формулах сил и энергий кулоновского взаимодействия.

В системе СГС результат выводится проще без необходимости введения диэлектрической постоянной вакуума. В СГС она равна просто 1.