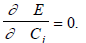
(1.5)

Чтобы получить величины коэффициентов Cj и энергию каждой МО (Ei), операцию (1.5) нужно провести на общей форме приближения ЛКАО 􀃆 МО, которая дается уравнением (1.2). Таким образом, подстановка уравнения (1.2) в уравнения (1.4), если опустить индексы (j) для МО, дает

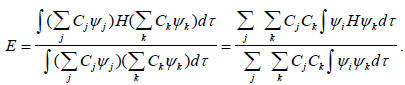
Примем следующие сокращенные обозначения:

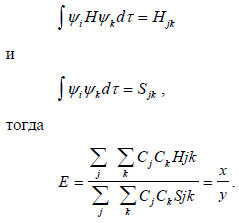
(1.6)

Далее, применяя уравнение (1.5), получаем

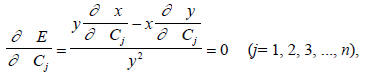
откуда после подстановки уравнения (1.6) имеем

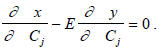
(1.7)

Дифференцируя x и y в уравнении (1.6) по Сj, получим

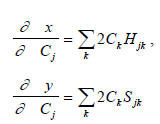
и из уравнения (1.7)

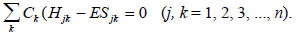
Это и есть вариационное уравнение. Конечным результатом применения вариационного принципа, который позволяет рассчитать коэфициенты С в уравнении (1.2), является система таких уравнений. Для аллильной π-системы, в которой j и k меняются от 1 до 3 и j отстается постоянной в каждом отдельном уравнении, вариационные уравнения имеют вид

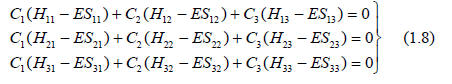
Систему уравнений (1.8) можно решить, составив секулярный детерминант

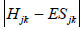
(уравнение 1.9) и решая его для величины Е. Затем значения Е подставляются в уравнения (1.8) и определяются Сij. Интегралы Hjk и Sjk нельзя точно вычислить, так как они получаются слишком сложными. Как раз с этого момента и начинаются расхождения между методом МОХ и более углубленными методами. Вместо попытки решить эти интегралы какими-либо приближенными способами в методе Хюккеля эти интегралы принимают постоянными параметрами, и энергия орбиталей выражается через них. В главе 2 при изложении метода ВМО в качестве меры энергии мы будем использовать постоянные значения кулоновского (α) и резонансного (β) интегралов.

Метод Хюккеля. Основные положения, на которых основан метод МОХ, применяемый для сопряженных π-систем, состоит в следующем:

1) Hjj = α;

2) Hjk = β, если атомы j и k связаны друг и другом,

и Hjk = 0, если атомы j и k не связаны;

3) Sjj = 1; Sjk = 0 для j ≠ k;

4) σ-связи локализованы, и их можно рассматривать как жесткий скелет, окруженный π-электронами.

Интеграл α, называемый кулоновским интегралом, представляет собой энергию электрона на С2р-орбитали. Если рассматривать лишь чисто углеродные системы, то предположение, что для всех атомов Hjj одинаковый, является хорошим приближением; при введении в молекулу π-системы гетероатома α уже не является постоянной величиной. Интеграл β обычно называют резонансным интегралом. Он представляет собой энергию взаимодействия двух атомных орбиталей на соседних атомах j и k. Предположение, что интеграл β всегда одинаков, довольно сомнительно, так как в сопряженных углеводородах степень взаимодействия двух АО может сильно меняться. Например, в бутадиене (рис. 1.23) взаимодействие между первым и вторым атомами углерода будет иным, чем взаимодействие между двумя внутренними атомами, так как длины связей между этими атомами сильно различаются.

Интеграл Sjk называется интегралом перекрывания; для j=k он равен 1. Поскольку для атомных орбиталей

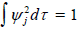
(условие нормировки; разд. 1.3), предположение, что Sjj =1, вполне оправдано. Однако предположение, что Sjk = 0 для j≠k, например, для соседних атомов (k = j +1), совершенно некорректно (по расчетам Робертса, в этом случае Sjk = 0.25).

Четвертое предположение - о том, что σ-связи локализованы, - по-видимому, вполне приемлемо.