Метод молекулярных орбиталей возник в результате применения квантовой механики к атомам и молекулам. Точное решение уравнений квантовой механики наталкивается на огромные математические трудности, и в настоящее время его можно получить только для самых маленьких атомов. В 1931 г. Э.Хюккель предложил метод обхода этих трудностей, введя в квантовомеханические уравнения вместо некоторых нерешаемых членов определенные параметры, характеризующие энергию МО.

Метод молекулярных орбиталей Хюккеля (метод МОХ) первоначально применялся исключительно для расчета π-орбиталей ненасыщенных углеводородов, но в 1963 г. Он был распространен Р.Гофманом на σ-орбитали под названием «расширенный метод Хюккеля» (РМХ). Метод Хюккеля относится к числу самых простых способов оценки энергии орбиталей и атомных коэффициентов. Несмотря на то, что в настоящее время развито много более точных методов, знакомство с этим простым методом может послужить хорошей иллюстрацией квантово-химического способа мышления и той формы, в которой получаются количественные результаты.

Вариационное уравнение. Квантовомеханическое описание атомов и молекул основано на уравнении Шредингера (разд. 1.1), которое обцчно записывают в форме

НΨ=ЕΨ (1.1)

где Н - оператор Гамильтона (гамильтониан); Ψ - волновая функция (собственная функция), описывающая орбиталь; Е - энергия данной собственной функции. Смысл такой записи состоит в том, что операция оператора над собственной функцией приводит к величине, кратной собственной функции. Например, если взять не оператор Гамильтона, а более простой оператор дифференцирования d/dx, то операция дифференцирования над собственной функцией есх, т.е. d/dx(ecx) даст сесх, т.е. величину, кратную есх. Это значит, что есх является собственной функцией оператора . С другой стороны, x не яляется собственной функцией оператора d/dx, так как d/dx(х) не кратно x. Оператор Гамильтона представляет собой оператор энергии. Современные математические методы не позволяют решить уравнение (1.1) даже для относительно простых молекул. Однако методом МОХ можно получать хорошие результаты, не вдаваясь в математическую форму Н или Ψ.

Чтобы получить Ψ, используют приближение, утверждающее, что линейная комбинация атомных орбиталей дает молекулярную орбиталь (ЛКАО 􀃆 МО).

Приближение ЛКАО 􀃆 МО:

(1.2)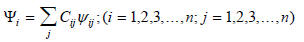

где Cij - коэффициент для каждой атомной орбитали ψj; i - номер рассматриваемой МО; j - номер атома в молекуле; n - число атомов в молекуле. Например, для аллильной π-системы (n=3) число π-орбиталей равно трем (ср. рис. 1.22):

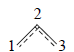
Ψ1=С12ψ1+С12ψ2+С13ψ3,

Ψ2=С21ψ1+С22ψ2+С23ψ3,

Ψ3=С31ψ1+С23ψ2+С33ψ3.

Теперь необходимо найти наилучшие значения коэффициентов С, чтобы Ψ были наилучшими приближениями к реальным орбиталям. Это делается с помощью вариационного принципа, который гласит, что любая волновая функция, не являющаяся строго корректной, приведет к значению энергии, численно большему его истинной величины. Чтобы этот принцип выразить в математической форме, нужно сделать следующие преобразования.

1. Умножить левую и правую части уравнения (1.1) на Ψ. Один из законов действий над операторами устанавливает, что ΨLΨ≠LΨ2, где L - некоторый оператор (например, xd/dx(x)≠d/dx(x2)). Поскольку Н - оператор, а Е - не оператор, в результате умножения получим

ΨНΨ=ЕΨ2

2. Проинтегрировать по всему пространству:

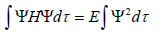
откуда энергия молекулярной орбитали

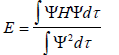
(1.3)

Согласно вариационному принципу, величина Е, полученная из уравнения (1.3), больше истинного значения Е, обозначаемого как Е0, поскольку Ψ - это приближенная орбиталь, полученная методом ЛКАО􀃆 МО.

Таким образом, математически вариационный принцип выражается уравнением

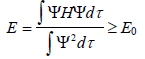
(1.4)

Чтобы Ψ была хорошим приближением к истинной орбитали (Ψ0) параметр Cj (в выражении 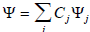; уравнение (1.2)) нужно выбрать так, чтобы Е была наименьшей. Это можно сделать, минимизируя Е по отношению к каждому из возможных коэффициентов: