После всего сказанного очевидно, что в методе МОХ используется так много сомнительных предположений, что он не может давать хорошие результаты. Тем не менее это не так: для чисто углеродных π-систем рассчитанные свойства очень хорошо согласуются с экспериментом. Исследования, проведенные М.Дьюаром, показали, что этот факт обусловлен удачным взаимным сокращением ошибок, а также характером молекул, к которым этот метод применим (сопряженные π-системы).

Используя предположения Хюккеля, для аллильной π-системы из уравнений (1.8) и (1.9) получаем

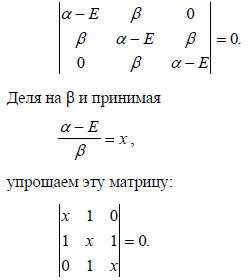
Далее этот детерминант разбиваем на (2х2)-детерминанты путем суммирования произведений каждого члена верхнего ряда на множитель, который определяется правилом: множитель j-го члена есть детерминант, полученный путем удаления j-й колонки и верхнего ряда матрицы:

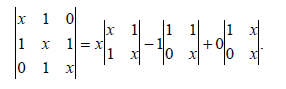
Заметим, что четные члены при разбиении матрицы всегда должны быть отрицательны. Детерминант типа (2х2) решаются простым перекрестным умножением и вычитанием произведений:

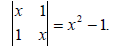
В результате получаем уравнение

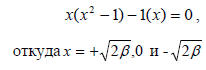
Таким образом, энергии аллильных π-орбиталей, измеренные относительно несвязывающего уровня α, будут иметь значения 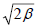, 0 и 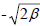, т.е. 1.41β, 0 и -1.41β. Отметим, что эти энергии очень близки к величинам, рассчитанным методом возмущений (1.5; 0 и -1.5; см. рис. 2.11 в гл.2).

Общая энергия π-электронов аллильной системы определяется выражением

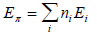
где ni = число элетронов на орбитали i. Следовательно,

где множитель 2 соответствует двум электронам на данной орбитали. Напомним, что α и β - отрицательные величины.

Энергию стабилизации (ΔЕπ) в результате сопряжения можно оценить сравнением с энергией локализованной системы с помощью уравнения

Елок=nπ(α+β)+niα,

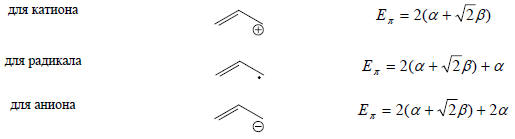
где nπ - число электронов на двойных свяях (для аллильной системы nπ = 2), а ni - число неподеленных электронов (для аллильного катиона - 0, для радикала - 1, для аниона - 2). Таким образом, для всех трех частиц - катиона, радикала и аниона -

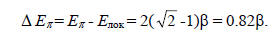
Коэффициенты можно определить подстановкой соответствующих значений Е в вариационное уравнение с применением условия нормировки

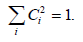
Для аллильной системы вариационные уравнения имеют вид

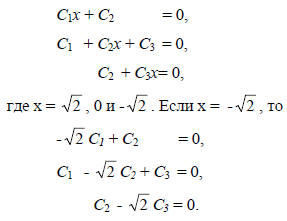
Из первого уравнения

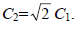
Подстановкой во второе уравнение получим

С1 = С3.

Условие нормировки дает

Следовательно,

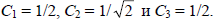
Таким образом, нижняя орбиталь аллильной π-системы имеет вид

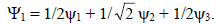
Решения для 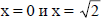дают две другие аллильные π-орбитали.