В предыдущем разделе мы уже получили многие важные соотношения, касающиеся момента импульса и его проекций. В этой главе будет доведено до конца решение задачи о квантовании момента количества движения пространственного ротатора и рассмотрены его свойства.

4.3.6.1

.Согласно (4.75), не существует состояния объёмного ротатора с . Поэтому при действии на волновую функцию с максимально возможным значением , т.е. , оператор повышения становится аннигилятором – "уничтожителем"

. (4.95)

Совершенно так же оператор уничтожает состояние с

.(4.96)

4.3.6.2.

Чтобы от оператора сдвига , не имеющего собственных значений, перейти к одному из операторов с конкретными собственными значениями и достаточно умножить (4.95) слева на и воспользоваться формулой (4.93):

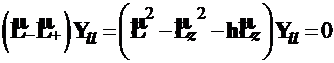.(4.96)

Отсюда на основании (4.64) и (4.91) следует

, т.е.

(4.98)

4.3.6.3.

В силу того, что постоянная определяет квадрат модуля момента импульса, она может быть только положительной величиной, либо равной нулю и, соответственно,

(4.99)

При дискретных допустимых значениях l

его минимальная величина равна нулю, а все остальные сдвигаются последовательно на единицу вверх

или (4.100)

4.3.6.4.

Этим охарактеризованы все свойства момента импульса при свободном вращении, а также и при вращательном движении на эквипотенциальной сферической поверхности. Квадрат модуля , сам модуль вектора и возможные его проекции на ось z

определяются формулами

, где , т.е. (4.101)

(4.102)

, где т.е. .(4.103)

Таким образом, всякому конкретному значению модуля момента импульса отвечает возможное значение проекции, т.е. каждому уровню вращательной энергии соответствует возможных состояний пространственного ротатора. Уровень, определяемый квадратом момента импульса , соответственно, кратно вырожден,