4.3.8.6.

Отметим, что мы не ставим перед собой и перед читателем задачу вывода общей формулы сферических волновых функций. Это связано, с одной стороны, с тем, что она обязательно покажется слишком перегруженной индексами и коэффициентами, к которым удобнее привыкать постепенно. С другой стороны, для практических целей редко требуются функции с большими значениями квантового числа l

. В химическом обиходе встречается состояния с l

= 0, 1, 2, 3, поэтому ограничимся этими значениями, (их символы см. в табл. 4.5 ).

4.3.8.7

. Итак, нас будут интересовать s–, p–, d–, f– орбитали жесткого ротатора. Запишем соответствующие исходные функции и , с точностью до постоянного множителя:

для s-состояния и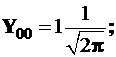

для p- состояния и

для d- состояния и

для f- состояния и

4.3.8.8.

Орбиталь s

–типа – лишь одна и волновая пункция требует только нормировки. Поскольку сомножитель 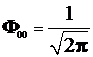уже нормирован, достаточно пронормировать функцию . Выделяя из элемента конфигурационного пространства (см. рис 4.3) все сомножители, определенные на переменной , получаем

и, соответственно, нормировочное соотношение имеет вид

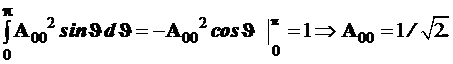(4.119)

Во всех дальнейших преобразованиях следующих двух разделов будем опускать постоянные численные коэффициенты перед волновыми функциями, получающимися в результате операций сдвигов состояний над исходными функциями – степенями синусоиды .

4.3.8.9.

Квантовое число l

=1 порождает три р-функции с m

=1, 0, -1 т.е. орбитали с Двум из них с отвечает Нормировочный множитель находим из соотношения

.

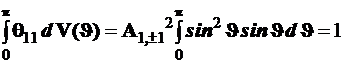Откуда следует: (4.120)

Функцию , необходимую для полного набора р-орбиталей, можно найти, сдвигая вниз или вверх на одно состояние

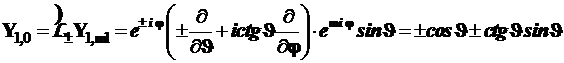
Определим нормировочный множитель для

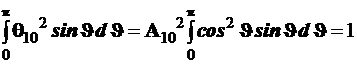
Интегрируя с помощью подстановки и, следовательно полагая, получаем