Совместные измерения динамических переменных. Коммутация операторов и соотношения неопределенностей Гейзенберга.

Вновь обратимся к анализу измерений. На основе результатов, полученных в разделах 2.2.3, 2.3.2 и 3.2.2, мы в состояниирешить очень важную проблему, связанную с совместными измерениями различных динамических переменных. Исследуем эту проблему на основе анализа операторных уравнений, имитирующих акты измерений. Последовательному измерению двух величин λ и μ соответствует произведение связанных с ними операторов и , т.е. их последовательное выполнение. Запись означает, что раньше измеряется величина μ, а затем λ. И, обратно, запись отвечает первичному измерению величины λ и затем – величины μ. Таким образом правило о последовательности выполнения операторов таково: произведение означает, что сначала на функцию действует оператор, стоящий непосредственно слева от функции, т.е. , в результате чего получается новая функция, над которой выполняется преобразование, диктуемое оператором .

Вопрос о совместности измерений двух величин сводится к тому, можно ли без последствий изменять порядок измерений. Если результаты не зависят от последовательности измерений, то операторные схемы и должны быть эквивалентными, а их разность будет нулевой:

, (3.61)

или, собирая влево от функции все операторы, получим:

. (3.62)

Формула (3.62) называется коммутационным (перестановочным) соотношением, а разность произведений операторов, записанных в разной последовательности, носит название коммутатора

. (3.63)

Коммутатор равен нулю для величин, которые могут наблюдаться одновременно. Коммутирующие операторы обладают одинаковыми наборами собственных функций. Если же коммутатор отличен от нуля, то совместное измерение величин не имеет смысла, т.е. такой прибор в принципе невозможно построить.

Рассмотрим одновременные измерения величин, у которых произведение их размерностей совпадает с размерностью константы Планка ([энергия]·[время]). Таковыми являются:

а) импульс и координата в одномерном поступательном движении;

б) проекция момента импульса на ось и точное положение, ротатора на орбите при плоском вращении, определяемом углом φ;

в) энергия и время у нестационарной системы.

Для этих трех случаев составим коммутаторы, пользуясь формулами (2.10), (3.24) и (2.19). На основании уравнения (2.19) оператор гамильтона можно заменить оператором 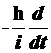. Получаем:

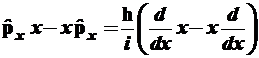, (3.64)

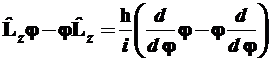, (3.65)

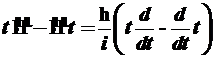(3.66)

В случае (3.66) волновая функция, на которую действует коммутатор, должна содержать временную часть.

Посмотрим, каков результат действий этих коммутаторов на волновую функцию на примере (3.64):

.

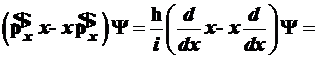
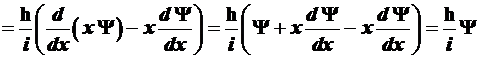Таким образом, исследуемый коммутатор равен

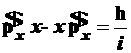. (3.67)

Согласно равенству (3.67), во всех математических выражениях, где можно произвести группировку операторов , приводящую к коммутатору, его можно заменить мнимым числом . Это же справедливо и для (3.65), и (3.66). Напомним, что операторы можно выносить только влево от функции и, производя преобразования, нельзя нарушать порядок сомножителей, но допустима группировка операторных слагаемых и сомножителей. Аналогично получаем:

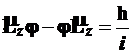, (3.68)

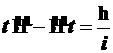. (3.69)

Формулы (3.67), (3.68) и (3.69) дают строгие операторные выражения принципа неопределенностей Гейзенберга, запрещающего одновременное точное измерение перечисленных пар переменных, и это принципиальное ограничение не связано с конструкцией прибора.