На полярных графиках гибридных орбиталей (рис. 6) наглядно представлена их ориентированность. Основная часть каждой орбитали сконцентрирована в больших лепестках, противоположно направленных в разные стороны от полюса – центра вращения.

Рассмотрим теперь более сложный случай σπ2-гибридных орбиталей. Полагая и выбирая для сi1 арифметическое значение корня, т.е. , мы неизбежно сохраняем свободу выбора значений сi2 и сi3, которая ограничена только условием

. (3.48)

Введем тригонометрическую постановку, удовлетворяющую условию (3.48):

, . (3.49)

Тогда общее выражение для гибридных орбиталей примет вид:

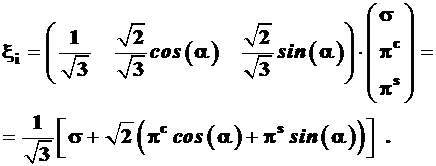(3.50)

Линейная комбинация орбиталей πс и πs в составе ξi представляет собой также πс-орбиталь, ось которой повернута под углом к исходному координат-ному лучу, так как:

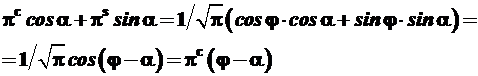. (3.51)

На этом основании из (3.50) получается общая формула для σπ2-гибридных волновых функций:

; i=1, 2, 3

Один из трех углов αi можно выбрать произвольно, но остальные будут определяться из условия ортогональности гибридных орбиталей. Без потери общности положим α1=0 и получим

, (3.53)

. (3.54)

Найдем углы α2,3, используя ортогональность гибридных функций (1.14):

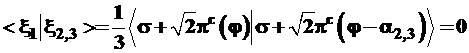
Откуда следует

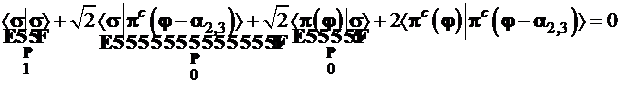и с учетом ортонормированности базиса, т.е. ‹σ|σ›=1; ‹σ|πс›=0 (независимо от ориентации πс-функции) получаем уравнение:

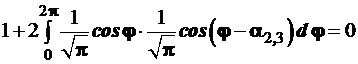
Совершим равносильные преобразования

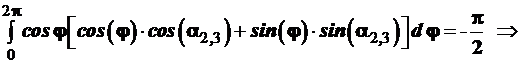
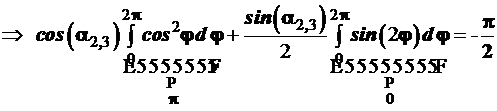
В итоге получаем искомое тригонометрическое уравнение

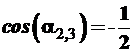и (3.57)

. (3.58)

Таким образом, все три гибридные орбитали ориентированны вдоль трех лучей, направленных под углом 1200 друг к другу.

Завершая расчеты волновых функций σπ- и σπ2-гибридов, изобразим полярные диаграммы гибридных орбиталей и уровни энергии.

Покажем, что энергия смешанного гибридного состояния отличается от энергий исходных чистых состояний и является их средневзвешенной величиной. Для расчета используем исходный гамильтониан плоского ротатора, для которого σ- π-орбитали являются собственными функциями.

Расчитывая уровни σπ- и σπ2-гибридов, мы имеем возможность продемонстрировать компактность и простоту математических выкладок, основанных на операторных уравнениях с использованием бра- и кет-символов скалярных произведений – интегралов.

Обратимся к 5-му постулату, на основании которого производится расчет средних значений динамических переменных. Энергия σπ-гибрида равна:

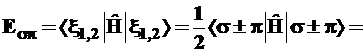
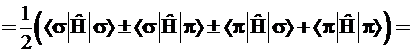
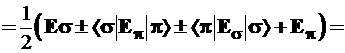
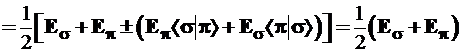. (3.59)

Уровень σπ-гибрида оказался дважды вырожденным и лежащим точно посередине между исходными уровнями σ- и π-орбиталей. При выводе использованно свойство ортонормированности базиса: ‹σ|σ›=1; ‹σ|π› = ‹π|σ› = 0

Энергия σπ2-гибрида рассчитывается аналогично; для краткости записи введем обозначение и получим:

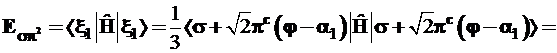
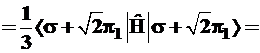
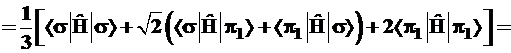
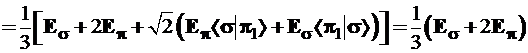(3.60)

Здесь гибридный уровень трижды вырожден и лежит ближе к π-уровню, котоpый представлен в формуле (3.60) со вдвое большим весом по сравнению с Еσ.

Информация, полученная нами в этом разделе, окажется очень полезной при качественном анализе химической. связи и теории валентности.