Для получения наиболее полной информации о механизме реакции необходимо вычислить многомерную поверхность потенциальной энергии (ППЭ), то есть рассчитать зависимость полной энергии от координат атомных ядер. Наиболее интересными и важными при изучении механизма реакции являются так называемые стационарные точки на ППЭ. Под этим термином понимают минимумы и седловые точки на ППЭ (рисунок 3.1.5.1, 3.1.5.2) В стационарных точках производные полной энергии по всем независимым координатам равны нулю.

Рисунок 2.1.5.1 Стационарные точки

а — минимум локальный или глобальный;

б — седловая точка

Рисунок 2.1.5.2 Простейшая ППЭ

Темные кружки – исходные

реагенты и продукты реакции;

крестик — переходное состояние.

В точке минимума полной энергии матрица вторых производных имеет только положительные собственные значения, а в седловой точке – одно отрицательное собственное значение. Минимумы полной энергии соответствуют устойчивым структурам и интермедиатам, а седловые точки – переходным состояниям.

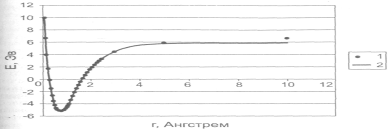
Рисунок 2.1.5.3. Зависимость потенциальной энергии молекулы водорода от расстояния между атомами: 1 — расчет полуэмпирическим методом РМЗ; 2 — аппроксимация потенциалом Морзе.

Типичный вид простейшей двумерной ППЭ показан на рисунке 2.1.5.2. Здесь минимумы соответствуют исходным реагентам и конечным продуктам реакции, а седловая точка – переходному состоянию. Минимумы на рисунке соединены пунктирной линией, которая проходит по дну долины на ППЭ через седловую точку. Эта линия показывает путь реакции в двумерном пространстве или траекторию движения реагентов в ходе реакции. Для большинства реакций ППЭ имеют более сложный вид.

В таблицах 1.7 и 1.8 приложения А сопоставлены данные расчета параметров переходных состояний для реакций, изображенных на схемах 1 - 5, методами МПДП и КМПДП (метод МПДП с учетом электронной корреляции), неэмпирическим методом в приближении Хартри – Фока без учета и с учетом электронной корреляции.

Схема I Схема II Схемa III

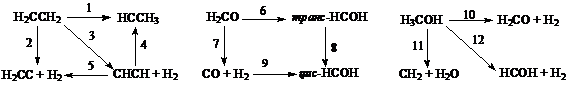
Схема IV Схемa V

В таблицах неэмпирический расчет в приближении Хартри – Фока без учета электронной корреляции обозначен ХФ, с учетом электронной корреляции – КХФ. Для реакций, изображенных на схемах 1 – 3, расчеты с оптимизацией геометрии в приближении Хартри – Фока проведены в базисе 6-31ГФ*, для реакций, изображенных на схемах 4, 5, - в базисе 3-21ГФ или 4-31ГФ. Электронная корреляция учитывалась только при вычислении энергии активации.

Из этих данных видно, что геометрические параметры переходных состояний, вычисленные методами МПДП и КМПДП, находятся в хорошем согласии с данными неэмпирических расчетов без учета электронной корреляции.

Вопрос о влиянии электронной корреляции на геометрию переходных состояний был рассмотрен в работе Шредера [20]. В ней методом МПДП без учета и с учетом электронной корреляции была рассчитана геометрия переходных состояний для реакций, изображенных на схемах 1 – 5, и показана хорошая сходимость с экспериментом.