Одним из наиболее значительных достижений электрохимии 60-х годов является построение диаграмм pH-потенциал для всех важных металлов, названных в честь автора диаграммами Пурбе.

Диаграммы характеризуют, прежде всего, состав водного раствора и термодинамическую устойчивость твердой фазы (металла, оксидов, гидрооксидов и других соединений) в зависимости от двух переменных – электродного потенциала φ и pH. Каждая диаграмма построена в предположении, что все другие переменные заданы, но изменение состава водного раствора по еще одной переменной, например по концентрации иона металла, можно отобразить семейством линий. На полных диаграммах pH-потенциал наносят семейства линий при активностях ионов в растворе, равных 100, 10-2, 10-4, 10-6М. Эти линии обозначают соответственно числами 0, -2, -4 и -6. Для характеристики коррозионных процессов используют упрощенные диаграммы Ph=-потенциал. Для этого или объединяют кривые, соответствующие разным активностям ионов в водном растворе, проводя усредненную кривую, или строят диаграмму только при =10-6М.

Для расчета и построения диаграмм pH-потенциал необходимо располагать сведениями о химических и электрохимических реакциях, возможных в данной системе, об их количественных термодинамических характеристиках (энергиях Гиббса, стандартных электродных потенциалах, их температурных коэффициентах).

В области низких температур (0 – 100°С) энергию Гиббса реакции достаточно рассчитывать в приближении Улига:

(1.3.1)

Величину стандартного электродного потенциала можно определить по уравнению

(1.3.2)

В справочной литературе стандартные потенциалы отнесены к температуре 298К, их величины при других температурах могут быть найдены из уравнения (1.3.2) или по соответствующим изотермическим температурным коэффициентам. Первый изотермический коэффициент отражает изменение стандартной энтропии электродной реакции:

(1.3.3)

а второй – изменение изобарных теплоемкостей

(1.3.4)

Если известны температурные коэффициенты, то стандартный потенциал любого электрода по температуре, отличной от 298К, можно рассчитать по уравнению

(1.3.5)

Приближение Улига (=0) соответствует уравнению (1.3.5) с учетом лишь первого температурного коэффициента.

Линии на диаграммах pH-потенциал рассчитывают по равновесию, представленному в общем виде:

(1.3.6)

для которого можно записать уравнение равновесного потенциала

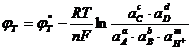(1.3.7)

Где - активности компонентов в конденсированных фазах. Если один из реагентов или продуктов реакции (1.3.6) находится в газовой фазе, то вместо термодинамической активности в уравнение (1.3.7) подставляется соответствующее парциальное давление (летучесть). Вводя общепринятое обозначение ,получим

(1.3.8)

Для того, чтобы по уравнению (1.3.8) построить линию на диаграмме pH-потенциал, из условий равновесия устанавливают значения и так, чтобы последний член имел определенную величину. Затем строят прямую линию с ординатой при pH=0 и наклоном . При 298К значение равно 0,0591 В, тогда наклон составит .

Наклонные линии (m≠0, n≠0) отображают равновесия, в которых участвуют ионы H+ или OH- совместно с электронами; горизонтальные линии (m=0, n≠0) – равновесия, в которых участвуют электроны, но не принимают участия ионы H+ и OH-; вертикальные линии (m≠0, n=0) – равновесия, в которых принимают участие ионы H+ и OH-, но не участвуют электроны. Последнее равновесие является химическим, поэтому не может быть рассчитано по формуле (1.3.7). Вместо него применяют

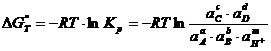(1.3.9)

Затем определяют pH для вертикальной линии: