Задача состоит в том, чтобы подобрать последовательность равновесий, которая бы удовлетворяла условию возрастания давления кислорода в системе. При этом возможно проводить варьирование значений энергий Гиббса образования силицидов в пределах возможных справочных значений.

После многократного согласования энергий Гиббса образования силицидов, взятых из различных источников, получен следующий вариант последовательности окисления.

1. Si – Mn11Si19 – SiO2; (I)

2. Mn11Si19 – MnSi – SiO2; (II)

3. MnSi– Mn5Si3– SiO2; (III)

4. Mn5Si3 – MnSiO3– SiO2; (IV)

5. Mn5Si3 – MnSiO3 – Mn2SiO4; (V)

6. Mn5Si3 – Mn5Si2 – Mn2SiO4; (VI)

7. Mn5Si2– Mn3Si – Mn2SiO4; (VII)

8. Mn3Si –Mn2SiO4 – MnO; (VIII)

9. Mn9Si2 – Mn3Si – MnO; (IX)

10. Mn0,85Si0,15 – Mn9Si2 – MnO; (X)

11. α – Mn0,85Si0,15– MnO; (XI)

12. MnO – Mn3O4 – Mn2SiO4; (XII)

13. Mn3O4 – Mn2SiO4 – MnSiO3; (XIII)

14. Mn3O4 – Mn2O3 – MnSiO3; (XIV)

15. Mn2O3 – MnO2 – MnSiO3; (XV)

16. MnO2 – MnSiO3 – SiO2; (XVI)

17. MnO2 – Mn2O7 – SiO2; (XVII)

18. Mn2O7–SiO2–{O2}; (XVIII)

Примеры расчета:

а) Фазовое равновесие III: MnSi– Mn5Si3 – SiO2

Уравнение реакции, соответствующее данному равновесию:

(1)

Константа равновесия реакции (1):

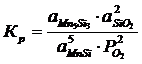; (2.1)

Мольные доли компонентов равны единице, поэтому выражение для константы равновесия упрощается:

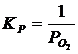; (2.2)

Уравнение изотермы химической реакции:

; (2.3)

Энергия Гиббса реакции (1) рассчитывается по формуле:

; (2.4)

С учетом уравнения (2.2):

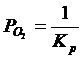
б) Фазовое равновесие X:

Mn0,85Si0,15 – Mn9Si2 – MnO

Уравнение реакции, соответствующее данному равновесию:

80Mn0,85Si0,15 + 7O2 = 6Mn9Si2 + 4MnO

Константа равновесия реакции (2):

;

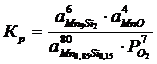Мольные доли компонентов равны единице, поэтому выражение для константы равновесия упрощается:

;

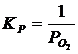Дальнейшие расчёты аналогичны предыдущему.

в) Фазовое равновесие XI:

α – Mn0,85Si0,15– MnO

Уравнение реакции, соответствующее данному равновесию:

2Mn(α)+O2=2MnO

Константа равновесия реакции (3):

;

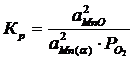Мольная доля чистого вещества равна единице, поэтому выражение для константы равновесия упрощается:

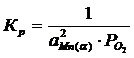(4)

Равновесие MnO с альфа-фазой является моновариантным, поэтому давление кислорода в газовой фазе, равновесной с конденсированной фазой, будет зависеть от активности марганца в альфа-фазе. Однозначно определить его можно, например, для точки, соответствующей предельной растворимости кремния в марганце. В этой точке мольная доля кремния , и .

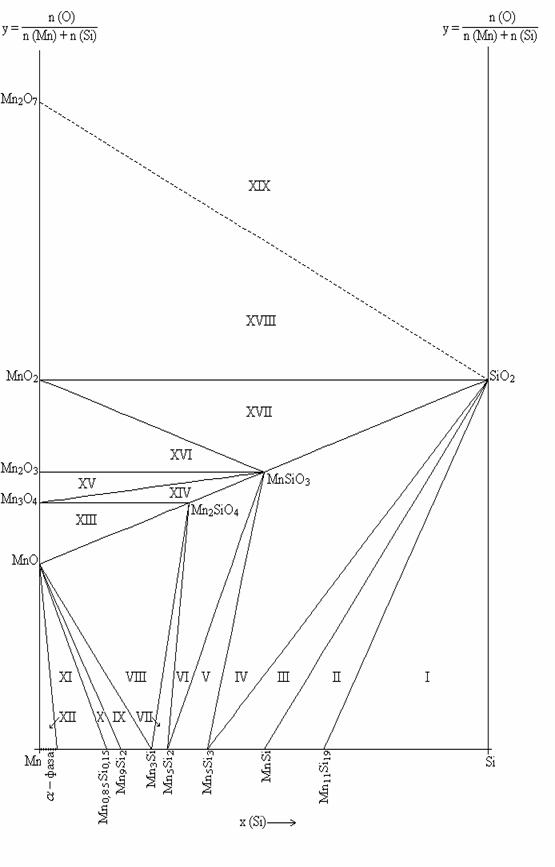
Рис.2.1. Фазовая диаграмма состояния системы Mn-Si-O при 25 0С.

Таблица 2.8 Характеристики фазовых равновесий системы Mn-Si-O при 25 0С