Как следует из экспериментальных данных по системе марганец-кремний (рис.1.1), кремний-кислород (рис.1.4) и марганец-кислород (рис.1.5) в системе Mn-Si-O можно предположить существование областей, в которых присутствуют следующие фазы (поскольку химическое сродство кремния к кислороду выше, чем марганца, то вероятнее, что почти при любом составе сплава Mn-Si в первую очередь будет реализовываться равновесие сплав – SiO2):

1. Si(γ) – Mn11Si19 – SiO2; (I)

2. Mn11Si19 – MnSi –SiO2; (II)

3. MnSi – Mn5Si3 – SiO2; (III)

4. Mn5Si3 – Mn5Si2 – SiO2; (IV)

5. Mn5Si2– Mn3Si – SiO2; (V)

6. Mn3Si – Mn9Si2 – SiO2; (VI)

7. Mn9Si2 – R(Mn6Si) – SiO2; (VII)

8. R(Mn6Si) – α-фаза – SiO2; (VIII)

9. α-фаза – SiO2; (IX)

10. α-фаза ––MnSiO3–SiO2; (X)

11. α-фаза ––Mn2SiO4–MnSiO3; (XI)

12. α-фаза ––MnO– Mn2SiO4; (XII)

13. MnO–Mn3O4– Mn2SiO4; (XIII)

14. Mn3O4– Mn2SiO4– MnSiO3; (XIV)

15. Mn3O4–Mn2O3– MnSiO3; (XV)

16. Mn2O3– MnSiO3–SiO2; (XVI)

17. Mn2O3–MnO2–SiO2; (XVII)

18. MnO2–Mn2O7–SiO2; (XVIII)

19. Mn2O7–SiO2–{O2}; (XIX)

Для того, чтобы однозначно определить инвариантное состояние системы, необходимо задать равновесные составы сосуществующих фаз и давление кислорода в газовой фазе, равновесной с конденсированными фазами.

Примеры расчета:

а) Фазовое равновесие V: Mn5Si2– Mn3Si – SiO2

Уравнение реакции, соответствующее данному равновесию:

(1)

Константа равновесия реакции (1):

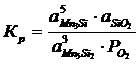; (2.1)

Мольные доли компонентов равны единице, поэтому выражение для константы равновесия упрощается:

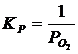; (2.2)

Уравнение изотермы химической реакции:

; (2.3)

Энергия Гиббса реакции (1) рассчитывается по формуле:

; (2.4)

С учетом уравнения (2.2):

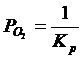
б) Фазовое равновесие X:

α-фаза ––MnSiO3–SiO2 было описано независимыми реакциями образования SiO2 и MnSiO3 из компонентов α-фазы (Mn, Si) и компонентов газовой фазы O2:

(1) ;

(2) ;

Константы равновесия реакций 1 и 2:

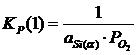; (2.3)

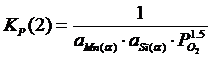; (2.4)

Для определения состава α-фазы исключим из конечного термодинамического уравнения. Для этого возведем уравнение (2.3) в куб и поделим полученное на уравнение (2.4), получим:

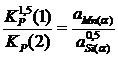; (2.5)

Это уравнение можно переписать в виде:

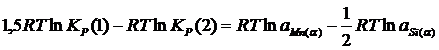; (2.6)

Из уравнения изотермы химической реакции:

; (2.7)

уравнение (2.3.4) можно переписать:

; (2.8)

Данное трансцендентное уравнение можно решить только численным методом. Обозначив , , получим:

; (2.9)

; (2.10)

Подставив уравнения (2.9) и (2.10) в (2.8) решаем численным методом, находим значение х. Исходя из уравнений (2.3) или (2.4) определяем величину .