Задав таким образом зависимости Q=f(T) как полиномы второй степени и зафиксировав один из параметров x, N, T, нужно решить систему (2.8). В этом случае система будет состоять из двух трансцендентных уравнений, и решить их совместно можно только численными методами. Автору работы не удалось этого сделать.

Поэтому было принято решение пожертвовать точностью аппроксимации функций Q=f(T) и определить их как линейные зависимости. В этом случае Q=aT+b и температура будет входить в уравнения системы (2.8) только в первой степени, что позволяет исключить её, как неизвестное.

Воспользуемся условными обозначениями, которые уже были использованы ранее.

Пусть , а . Тогда первое уравнение системы (2.9) запишется в виде:

(2.15)

Если перенести все слагаемые, содержащие Т, в левую часть, а все остальные – в правую часть уравнения, то получится:

(2.16)

Осталось только выразить температуру в явном виде:

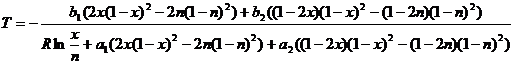(2.17)

Аналогично нужно выразить температуру и из второго уравнения системы (2.9):

(2.18)

(2.19)

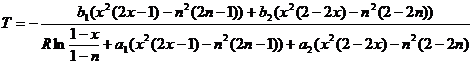(2.20)

Приравняв правые части равенств (2.17) и (2.20) и умножив их на -1, приведём уравнение к окончательному виду:

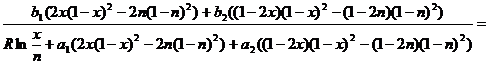
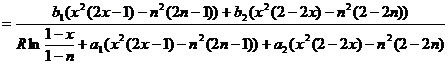(2.21)

Параметра а и b определим из данных таблицы 2.4. Чтобы решить трансцендентное уравнение (2.21), нужно задаться одним из параметров x, или n и численными методами подобрать второй параметр, а затем определить и температуру по любому из уравнений (2.17) или (2.20).

Для решения была использована надстройка «поиск решения» пакета Microsoft Excel. Результаты решения представлены в таблице 2.5.

Табл. 2.5. Рассчитанный купол расслаивания твёрдого раствора при разных температурах