Расчёт зависимости энергий смешения компонентов системы Cu – Ni от температуры
Дипломы, курсовые и прочее / Определение термодинамических активностей компонентов бронзы БрБ2 / Дипломы, курсовые и прочее / Определение термодинамических активностей компонентов бронзы БрБ2 / Расчёт зависимости энергий смешения компонентов системы Cu – Ni от температуры Расчёт зависимости энергий смешения компонентов системы Cu – Ni от температуры
Страница 2

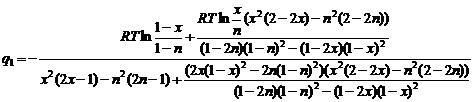(2.12)

Теперь приведём выражения в числителе и знаменателе дроби (2.12) к общему знаменателю:

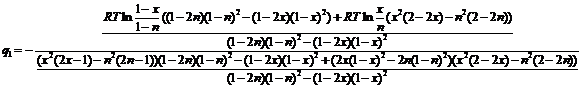
(2.13)

Умножив числитель и знаменатель дроби (2.13) на выражение , окончательно получим:

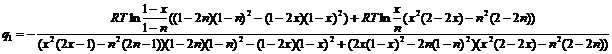
(2.14)

Система уравнений (2.9) не имеет степеней свободы, поэтому случайная погрешность отсутствует. Возможно, пользуясь законом накопления ошибок, определить систематическую погрешность и рассчитать доверительный интервал для значений Q. В данной работе это не учитывается.

Координаты купола расслаивания при различных температурах были сняты с диаграммы состояния Cu – Ni (рис. 1.7) и представлены в таблице 2.1.

Табл. 2.1. Координаты купола расслаивания твёрдого раствора при разных температурах.

t, oC

Состав α-фазы (Cu)

Состав γ-фазы (Ni)

x1

x2

N1

N2

200

0,650

0,350

0,013

0,987

225

0,633

0,367

0,027

0,973

250

0,580

0,420

0,053

0,947

275

0,513

0,487

0,073

0,927

300

0,467

0,533

0,113

0,887

325

0,387

0,613

0,187

0,813

342

0,300

0,700

0,300

0,700

Для каждой из температур были проведены вычисления значений энергий смешения. вычислены по формуле (2.14), а при известной по формуле (2.10). Для вычислений была использована компьютерная программа, текст которой приведён в приложении А.

Страницы: 1 2 3

Смотрите также

Фармацевтический анализ производных фенотиазина
Фенотиазины - исторически первый класс антипсихотических средств - по своей химической структуре представляют собой трициклические молекулы. Все фенотиазины подразделяются на три основн ...

Основные химические законы
Когда впервые обнаруживается, что некоторая идея объясняет или коррелирует многие факты, то такую идею называют  гипотезой. Гипотезу можно подвергнуть дальнейшей проверке и экспериментально ...

Современные тенденции и новые направления в науке о полимерах
Современные тенденции и новые направления в науке о полимерах ярко проиллюстрированы в рамках исследований проведенных Российским Фондом Фундаментальных Исследований (РФФИ) В настоящее в ...