Рассмотрим низкотемпературную часть диаграммы Cu – Ni (см. рис. 1.7). Ниже линии солидуса образуется ряд непрерывных твёрдых растворов с решёткой ГЦК. Однако при температурах ниже 342°С наблюдается купол расслаивания на твёрдый раствор на основе меди (обозначим его, как α-фазу) и твёрдый раствор на основе никеля (обозначим его, как γ-фазу). Внутри купола находится смесь этих фаз.

На границе купола α-фаза находится в равновесии с γ-фазой. Это можно записать следующими уравнениями:

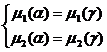(2.4)

Для любого из компонентов 1 и 2 и в α- и в γ-фазе справедливо соотношение:

(2.5)

Обе фазы имеют одинаковую структуру (ГЦК). Это можно объяснить высоким сродством меди и никеля. На диаграмме состояния (рис. 1.7) видно, что сплав плавится конгруэнтно во всём диапазоне концентраций. Более того, линии ликвидуса и солидуса расположены очень близко друг к другу, то есть плавление происходит почти в изотермических условиях, как у чистого металла. Аналогично происходит и испарение сплава.

На основании этого можно записать, что:

(2.6)

Тогда система (2.4) перепишется в виде:

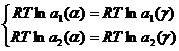(2.7)

Обозначим через х мольные доли компонентов в α-фазе, а через N – мольные доли компонентов в γ-фазе, и учитывая условия нормировки их на единицу, можно систему уравнений (2.7) с учётом (1.3) и (1.6) переписать в следующем виде:

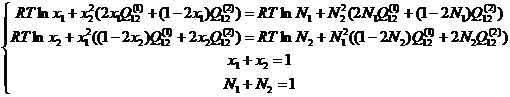(2.8)

Если бы были известны мольные доли x и N при 25°С, то можно было бы с помощью (2.8) непосредственно вычислить значения Q при этой температуре. Однако при столь низкой температуре невозможно получить экспериментальных данных о координатах купола расслаивания. Дело в том, что наступление равновесия между фазами происходит, благодаря диффузии атомов, а в комнатных условиях она протекала бы экстремально долго (несколько сотен лет). Поэтому необходимо изучить температурную зависимость энергий смешения и экстраполировать её на уровень комнатных температур.

Если T=const и известны все x и N, то система уравнений (2.8) линейна относительна параметров Q и может быть решена аналитически.

Обозначим . Если теперь перенести правую часть системы (2.8) в левую, то она перепишется в виде:

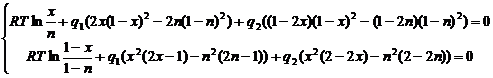(2.9)

Выразим из первого уравнения системы (2.9):

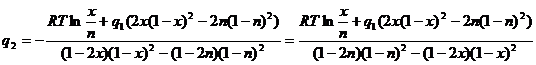(2.10)

Подставим (2.10) во второе уравнение системы (2.9):

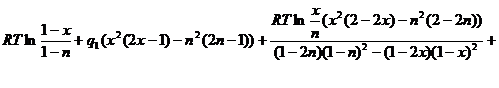
(2.11)

Теперь можно выразить в явном виде величину :