Меню сайта
Наши новости
Распространение алкалоидов в растительном мире.
Умягчение воды
Алгоритмы вывода кинетических уравнений для стационарных и квазистационарных
процессовСтатьи и работы по химии / Алгоритмы вывода кинетических уравнений для стационарных и квазистационарных процессов / Статьи и работы по химии / Алгоритмы вывода кинетических уравнений для стационарных и квазистационарных процессов / Алгоритмы вывода кинетических уравнений для стационарных и квазистационарных
процессов Алгоритмы вывода кинетических уравнений для стационарных и квазистационарных
процессовСтраница 4
W1 = R1, W2 = R1, W3 = R1 + R2, W4 = R2
(для маршрутов I и II)
Используем алгоритмы Яблонского (64) и Мезона (62). Для обоих уравнений нужны величины Di. Запишем для каждой вершины i произведения сумм весов стадий, выходящих из всех других вершин КГ j ¹ i. Перемножим скобки и исключим из полученных сумм произведения стадий, образующих цикл, включая произведения ![]() . В результате получим Di. Для графа КГ6 запишем произведения сумм весов стадий:
. В результате получим Di. Для графа КГ6 запишем произведения сумм весов стадий:
![]()
Здесь нет циклов и ![]() .
.
![]()
![]()
![]()
Здесь два цикла ![]() и
и ![]() . Поэтому исключим их:
. Поэтому исключим их:
![]()
Таким образом, в КГ6 девять деревьев, величины которых войдут в SDi.
Для использования уравнения (64) надо найти величины циклов Сpn, проходящих через стадию, определяющую скорость RP (p – номер маршрута, n – номер цикла), и величины подграфов Dpn, которые являются корневыми определителями графов в вершине pm, образующихся при сжатии цикла n в одну вершину pn. В случае, когда после сжатия цикла остается одна вершина Dpn = 1. Итак, выбираем R1 = W2 и R2 = W4. В реакциях на поверхности [M]S = 1 (![]() ).
).
![]() (67)
(67)
Величина цикла равна произведению весов стадий. Тогда:
![]() D11 = 1
D11 = 1
![]() D12 = 1
D12 = 1
![]() (68)
(68)
![]() (69)
(69)
![]()
![]()
![]() D22 = 1
D22 = 1
![]() (70)
(70)
Получим уравнение для R2 по правилу Мезона (62), т.е. уравнение идентичное уравнению (70).
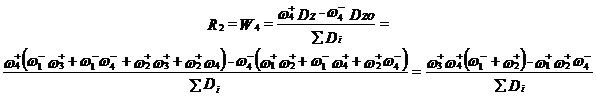
Смотрите также
Флотационный метод получения хлористого калия из сильвинита
Разработка и применение различных
методов обогащения калийных и полиметаллических руд неразрывно связаны с
минеральным составом исходной руды.
Выделить ценные компоненты из руд в богатый
...
Исследование электрохимического поведения ионов самария в хлоридных и хлоридно-фторидных расплавах
...
Углеводы как главный источник энергии в организме человека
...


