Меню сайта
Наши новости
Распространение алкалоидов в растительном мире.
Умягчение воды
Связи м/у активностями компонентовСтатьи и работы по химии / Активность. Порядок реакций / Статьи и работы по химии / Активность. Порядок реакций / Связи м/у активностями компонентов Связи м/у активностями компонентов
Уравнение Дюгема-Маргулиса:
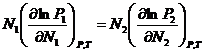(1). Если раствор является близким к совершенному, то 
, а 
. 
, 
. Продифиринцируем (
и 
=const) 
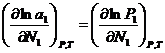(2), 
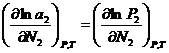(3). Подставим 
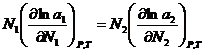(4). Уравнение (4) может быть обобщено на раствор, содержащий несколько компонентов: 
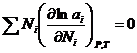. Если раствор близок к разбавленному 
для растворённого вещ-ва 
. Повторяя действие, что и здесь справедливо уравнение (4). Для бинарного раствора уравнение (4) имеет вид: 
, 
, 
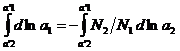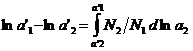. Если известна зависимость активности второго компонента от концентрации, а так же активность первого компонента для какой либо концентрации, то можно активность компонента для другой концентрации. Зная 
, можно подсчитать 
.
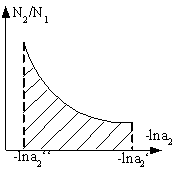
Смотрите также
Фальсификация бензинов
Фальсификация в России автомобильного топлива - национальная
традиция. Говорят, сейчас только в странах Западной Европы можно заправиться
настоящим бензином, отвечающим всем необходимым тр ...
Монослой на
основе фуллеренов и краун-эфиров
Проведенные
исследования [3-5] показали, что молекулы С60 при степени покрытия 0,4-0,5
начинают агрегировать уже в газовой фазе, что исключает возможность
формирования монослоя и, как следствие, во ...
Флотационный метод получения хлористого калия из сильвинита
Разработка и применение различных
методов обогащения калийных и полиметаллических руд неразрывно связаны с
минеральным составом исходной руды.
Выделить ценные компоненты из руд в богатый
...