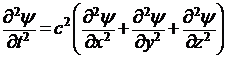, (6)

После исключения t (с помощью (3)) волновое уравнение примет вид:

, (7)

где ψ – так называемая волновая функция

– величина, периодически изменяющаяся по закону гармонического движения;

ν2 – оператор Лапласа, означающий, что над функцией производится следующее действие:

.

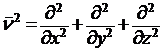Будем считать, что волновое уравнение (7) описывает движение частицы. Тогда λ

– длина фазовой волны

, а ψ

– амплитуда фазовой волны

в любой произвольно взятой точке χ, y, z, характеризующей местоположение частицы. Длину и амплитуду фазовой волны можно связать с массой и энергией частицы. Если частица движется в потенциальном поле, то ее полная энергия Е складывается из кинетической энергии Ек = mV2/2 и потенциальной энергии Еп. Отсюда

½mV2 – Е – Еп или m2V2 = 2m(E – Eп).

Учитывая соотношение де Бройля, запишем

m2V2 = h2/λ2 и λ2 = h2/2m (E – Eп)

и представим волновое уравнение в следующем виде:

(8)

В этой форме волновое уравнение называется уравнением Шредингера

. Оно является основным уравнением квантовой механики.

Уравнение Шредингера – дифференциальное уравнение в частных производных и может иметь множество решений. Однако физический смысл имеют лишь те ψ-функции (так называемые собственные функции

), которые удовлетворяют ряду условий. Во-первых, эти функции должны быть непрерывными, конечными, однозначными и обращаться в нуль на бесконечном расстоянии. Наложение перечисленных условий называется нормированием ψ-функции. Во-вторых, собственным ψ-функциям соответствуют не любые, а только дискретные значения полной энергии Е. Как дискретные значения энергии, так и вид собственных ψ-функций определяется совокупностью квантовых чисел n, l, m, которые хотя и не содержатся в самом уравнении Шредингера, но вводятся в него при решении. Таким образом, квантование энергии естественно и неизбежно вытекает из основных свойств материальных объектов и не нуждается в особом постулировании, которое было сделано Н. Бором при разработке планетарной модели атома.