Химические процессы сводятся к превращению молекул, т.е. к возникновению и разрушению связей между атомами. Поэтому важнейшей проблемой химии всегда была и остается проблема химического взаимодействия, тесно связанная со строением и свойствами вещества. Современная научная трактовка вопросов химического строения и природы химической связи дается квантовой

механикой

– теорией движения и взаимодействия микрочастиц (электронов, ядер и т.д.).

Одним из общих свойств материи является ее двойственность. Частицы материи обладают одновременно и корпускулярными и волновыми свойствами. Соотношение "волна – частица" таково, что с уменьшением массы частицы ее волновые свойства все более усиливаются, а корпускулярные – ослабевают. Когда же частица становится соизмеримой с атомом, наблюдаются типичные волновые явления. Одновременно оказывается невозможным описание движения и взаимодействия микрочастиц-волн законами движения тел с большой массой. Первый шаг в направлении создания волновой, или квантовой механики, законы которой объединяют и волновые, и корпускулярные свойства частиц, сделал де Бройлем (1924). Де Бройль высказал гипотезу, что с каждой материальной частицей связан некоторый периодический процесс. Если частица движется, то этот процесс представляется в виде распространяющейся волны, которую называют волной де Дройля

, или фазовой волной

. Скорость частицы V связана с длиной волны λ соотношением де Бройля

:

(1)

где m – масса частицы (например, электрона);

h – постоянная Планка.

Уравнение (1) относится к свободному движению частиц. Если же частица движется в силовом поле, то связанные с ней волны описываются так называемой волновой функцией

. Общий вид этой функции определил Шредингер (1926). Найдем волновую функцию следующим путем. Уравнение, характеризующее напряженность поля Еа плоской монохроматической волны света, можно записать в виде:

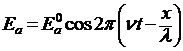, (2)

где Еа0 – амплитуда волны;

ν – частота колебаний;

t – время;

λ – длина волны;

х – координата в направлении распространения волны.

Так как вторые производные от уравнения плоской волны (2), взятые по времени t и координате х, равны соответственно:

, (3)

, (4)

то

Подставляя λ=с/ V (с – скорость света), получаем волновое уравнение для плоской световой волны:

, (5)

Последующие преобразования основываются на предположениях, что распространение волн де Бройля описывается аналогичным уравнением, и что эти волны становятся стационарными и сферическими. Сначала представим, что по уравнению (5) изменяется значение новой функции ψ от координат (χ, y, z), имеющей смысл амплитуды некоторого колебательного процесса. Тогда, заменяя Еа на ψ, получим волновое уравнение в форме: