В 1873 г. Ван-дер-Ваальс на основе молекулярной модели несжимаемых шаров диаметра D, притягивающих друг друга и притягиваемых друг другом, вывел свое удивительно простое уравнение. В реальном газе в результате молекулярного притяжения увеличивается кинетическое давление по сравнению с давлением в идеальном газе. Из самых общих соображений молекулярное притяжение пропорционально числу как притягивающих, так и притягиваемых молекул; Δp ~ N2. В результате молекулярного отталкивания свободный объем в реальном газе меньше, чем объем сосуда занимаемого газом. Запрещенный объем вокруг каждой молекулы, в который не может попасть центр другой молекулы из-за взаимного отталкивания, Ван-дер-Ваальс оценил как объем сферы , где D - расстояние между центрами двух несжимаемых шаров диаметра D. Следовательно, полный запрещенный объем моля газа будет равен , т.е. равен учетверенному объему Na несжимаемых молекул.

Уравнение Клапейрона для идеального газа - pV=NakT.

Уравнение Ван-дер-Ваальса представляет собой уравнение Клапейрона, в которое введены перечисленные выше поправки на возросшее вследствие межмолекулярного взаимодействия кинетическое давление и уменьшенный реальный свободный объем:

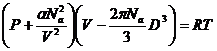 или  ,

где a – постоянная, b»4V0 (V0 – объем молекулы).

Если в качестве переменных P, V и T использовать их относительные значения Pc=P/Pk , Tc=T/Tk , Vc=V/Vk (где Pk, Tk, Vk – критические значения), то закон Ван-дер-Ваальса принимает вид универсального закона соответственных состояний:

Pc=F(Vc, Tc) — универсальная функция,   — универсальная постоянная.

Следствие из этого закона может быть сформулировано следующим образом: все вещества кипят при одних и тех же относительных давлениях и температурах. Или еще: относительные объемы всех веществ одинаковы при одних и тех же относительных давлениях и температурах. Уравнение Ван-дер-Ваальса можно записать и в другом виде:

,

т.е. представить в виде разложения потенциала притяжения по обратным степеням температуры, в котором учтен только первый член. Оправданием такого приближения служит предположение Ван-дер-Ваальса о дальнодействующем характере сил притяжения. В случае дальнодействия можно считать, что при переходе от одной конфигурации молекул к другой их потенциальная энергия не изменится, т.е. a=const вследствие того, что они находятся в среднем поле соседей с постоянной плотностью энергии.

Математическое и экспериментальное исследования этого уравнения показали, что поправки Ван-дер-Ваальса обладают глубоким физическим смыслом. Они качественно описывают не только изменения свойств системы, определяющих фазовый переход газ-жидкость, но и форму критической области. Кроме того, если силы притяжения нельзя рассматривать постоянными из-за близкодействия, то уравнение Ван-дер-Ваальса допускает следующее приближение с учетом члена 1/T2.

Ван-дер-Ваальс в 1873 году одним из первых указал на наличие нехимического межмолекулярного взаимодействия в аморфных состояниях вещества и разделил это взаимодействие на дальнодействующее притяжение и близкодействующее отталкивание. При этом, он предложил до сих пор самую простую, но в тоже время достаточно точную в широком интервале температур и давлений, математическую модель для учета вышеперечисленных сил при расчете состояний реального газа. В связи с вышеуказанными обстоятельствами дальнодействующие силы межмолекулярного притяжения и близкодействующие силы межмолекулярного отталкивания назвали силами Ван-дер-Ваальса.