. (4. I)

4.1.2.4. В самом простом случае для разделения переменных в уравнении (4.1) необходимо, чтобы оператор допускал группиров­ку всех выражений и действий над каждой из переменных в отдельные слагаемые, например и . Вводимые нами символы операторов красноречиво указывают на преобразуемые ими переменные и не требу­ют дополнительных пояснения. Итак, оператор должен быть пред­ставлен в аддитивной форме

(4.2)

Для разделения переменных в дифференциальном уравнении (4.1) искомую функцию F(x,y) следует представить в виде произведения двух сомножителей X(x) и Y(у), каждый из ко­торых является неизвестной функцией лишь одного аргумента:

, (4.3)

или

4.1.2.5. Аддитивный характер оператора и мультипликативная структура функции позволяет разделить переменные в дифференциальном уравнении (4.1). Подставив в него (4.2) и (4.3), получим

(4.4)

Дальнейшая процедура состоит в следующем:

слева умножаем выражение (4.4) на ;

преобразуем дифференциальное уравнение (4.4), учитывая, что операторы и не затрагивают чужую переменную и не изменяют функции от неё;

производим сокращения и

разделяем переменные.

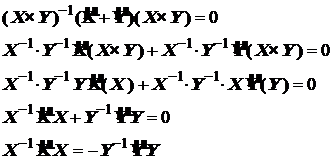
или (4.5)

4.1.2.6. В силу независимости аргументов функций X и Y, а также и преобразований над ними, выражение (4.5) следует приравнять посто­янной величине, а именно

(4.6)

Цепочка равенств (4.6) – это не что иное, как система двух дифференциальных уравнений, связанных между собой лишь постоянной , которая в каждой конкретной задаче находится из дополнительных математических или физических условий. Систему можно записать так

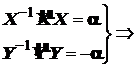
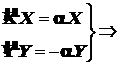
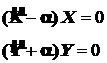(4.7)

Каждое из дифференциальных уравнений системы (4.7) включает лишь одну переменную и решается самостоятельно.

4.1.2.7. Такая схема легко распространяется на конфигурационное пространство В таком случае общее выра­жение для дифференциального уравнения (4.1) выглядит следующим образом

. (4.8)

4.1.2.8. Одномерные операторы–слагаемые , на которые разлагается многомерный оператор , с одной стороны, построены на разных переменных, а с другой стороны, могут иметь разную конструкцию, хотя это и не обязательно. Последнее их отли­чие отметим ниже индексами a,b,c . Основное условие возможно­сти разделения переменных выражается формулой, определяющей адди­тивную структуру оператора

(4.9)

4.1.2.9. Аддитивность оператора (4.9) порождает мультиплика­тивность решения уравнения (4.8), т.е.