Меню сайта
Наши новости
Распространение алкалоидов в растительном мире.
Умягчение воды
Возмущение первого и второго порядкаОрганическая химия / Внутри- и межмолекулярные взаимодействия / Органическая химия / Внутри- и межмолекулярные взаимодействия / Возмущение первого и второго порядка Возмущение первого и второго порядкаСтраница 1
Односторонний процесс между молекулами Д (донор) и А (акцептор) можно выразить следующей схемой:
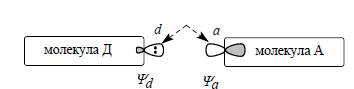
На этой схеме обоюдоострая пунктирная стрелка означает взаимное возмущение орбиталей, которые локализованы на атоме d молекулы Д и атоме а молекулы А.Возмущение молекулярных орбиталей при образовании комплекса Д А совершенно аналогично возмущению атомных орбиталей при образовании молекулы из атомов. Аналогично тому, как молекулярные орбитали представляются в виде линейной комбинации атомных орбиталей, орбитали комплекса Д
А совершенно аналогично возмущению атомных орбиталей при образовании молекулы из атомов. Аналогично тому, как молекулярные орбитали представляются в виде линейной комбинации атомных орбиталей, орбитали комплекса Д А являются линейной комбинацией взаимодействующих орбиталей молекул Д и А.При возмущении орбиталей ψа и ψd получаются две возмущенные орбитали Ψ+ и Ψ-, относящиеся к супермолекуле А←Д. Эти орбитали строятся на основе следующего правила.Правило 1. При образовании возмущенной нижней орбитали базисные орбитали объединяются с одинаковыми знаками, и в районе их взаимодействия будет связывание. При образовании возмущенной верхней орбитали базисные орбитали объединяются с разными знаками (относительными), и в результате будет антисвязывание:
А являются линейной комбинацией взаимодействующих орбиталей молекул Д и А.При возмущении орбиталей ψа и ψd получаются две возмущенные орбитали Ψ+ и Ψ-, относящиеся к супермолекуле А←Д. Эти орбитали строятся на основе следующего правила.Правило 1. При образовании возмущенной нижней орбитали базисные орбитали объединяются с одинаковыми знаками, и в районе их взаимодействия будет связывание. При образовании возмущенной верхней орбитали базисные орбитали объединяются с разными знаками (относительными), и в результате будет антисвязывание:

Если обозначить энергию орбитали ψd как αd, энергию ψа - как αа, а символом Е обозначить энергии возмущения орбиталей Ψ+ и Ψ-, то по теории возмущений (αd -E)(αa -E) = (β-SE)2, (2.5) где β - резонансный интеграл (рис. 2.1, б), характеризующий силу взаимодействия ψа и ψd на данном расстоянии, S - интеграл перекрывания, характеризующий степень перекрывания взаимодействующих орбиталей.
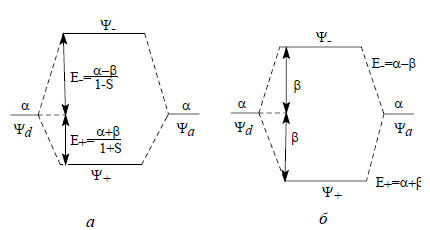
Рис. 2.1. Взаимное возмущение орбиталей ψа и ψd первого порядка с учетом перекрывания (а) и без учета перекрывания (б) Возмущение первого порядка. В случае вырожденных (одинаковой энергии) орбиталей ψd и ψа αd =αа =α и поэтому (α -E) = ±(β-SE), откуда, учитывая, что α и β - отрицательные величины, получаем
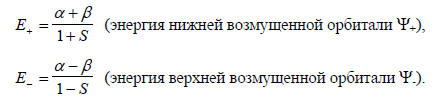
Поскольку интеграл перекрывания всегда положителен, (1+S)>(1-S), т.е. нижняя возмущенная орбиталь менее связывает Д и А, чем верхняя возмущенная орбиталь разрыхляет эту связь (рис. 2.1, а).Очень часто используют упрощение, заключающееся в пренебрежении интегралом перекрывания, т.е. принимают, что S=0. Тогда (рис. 2.1, б) Е = α±β, (2.6) т.е. исчезает асимметрия расщепления уровней.Волновые функции Ψ+ и Ψ- имеют вид Ψ+= Cdψd + Caψa, Ψ- = C*dψd - C*aψa, где C и C* - коэффициенты, с которыми входят орбитали ψd и ψa в орбитали Ψ- и Ψ+. Для возмущения первого порядка все коэффициенты одинаковы: Cd = C*d = Ca = C*a = 1/2. Эта величина возникает из условия нормировки (гл. 1, разд. 1.3), согласно которому для каждой орбитали 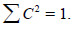 .
.
Смотрите также
Вода в химической промышленности
...
Определение содержания германия в твердом электролите GeSe-GeJ2
...
Разработка урока по теме: "Метан, его строение и валентные состояния атома углерода"
Цели урока: сформировать представление о составе и строении
метана, его нахождении в природе и физических свойствах; изучить валентные
состояния атома углерода.
Задачи урока: 1) изучить с ...


