Любое свойство объекта, любое явление квантовано, все в мире квантовано, включая само пространство. В этом заключается основной принцип квантовой механики. Энергия объекта не может измениться на произвольную величину. Объект может обладать лишь определенными значениями энергии, и нельзя сделать так, чтобы он имел какую-то промежуточную энергию. Это, между прочим, и явилось причиной введения уравнения Шредингера, которое вместе с предложенной выше интерпретацией волновой функции успешно объясняет квантование энергии. В разделе 1.1 указывалось, что для согласия с принципом квантования некоторые из бесконечного числа решений уравнения Шредингера нужно исключить. Это можно сделать на основе вероятностной интерпретации волновой функции.

Ограничение на волновые функции можно наложить с помощью простого заключения, состоящего в том, что если ψ2dx или ψ2dτ есть вероятность найти частицу в области dx или dτ, то сумма таких вероятностей по всему пространству должна быть равна единице. Это следует из того, что частица, если она существует, определенно где-то находится, пусть даже она «размыта» по всей вселенной. Таким образом, возникает критерий полной вероятности (по-иному его называют «условие нормировки»), который налагает жесткие ограничения на волновые функции, ибо ему удовлетворяют не все решения уравнения Шредингера, а только волновые функции, нормированные к единице, когда

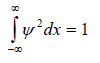
для одномерного движения или

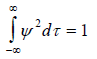
для трехмерного движения, где x - длина, а τ - объем.

Чтобы пояснить это, опять обратимся к атому водорода. В основном состоянии волновая функция пропорциональна exp(-r/a0) (см. предыдущий раздел), т.е. спадает по экспоненциальному закону при удалении от ядра. Однако интегрируя по всему пространству, можно вычислить, что условию нормировки, т.е. критерию полной вероятности, удовлетворяют не любые коэффициенты пропорциональности А в уравнении ψ=Aexp(-r/a0), а только один (называемый нормировочным множителем N), A=N=(1/πa03)1/2, который и был использован в предыдущем разделе при расчетах вероятности найти электрон на разных расстояниях от ядра. При других значениях А критерий полной вероятности не соблюдается и эти решения уравнения Шредингера неприемлемы. Если эти решения неприемлемы, то их отбрасывают, и тогда в уравнении Шредингера полная энергия Е электрона в атоме водорода не может иметь значения, соответствующие этим неприемлемым решениям. Так мы приходим к квантованию и теперь должны заявить, что возможны только некоторые значения энергии электрона в атоме водорода, поскольку другие значения соответствуют неверным свойствам распределения электрона в пространстве.