Очевидно

xidm + mdxi = yidm

mdxi = (yi – xi) dm

; где dt = d(lnm) 3.3

Очевидно, если dt >0 , то d(lnm) >0 и вещество приходит в жидкую фазу, если dt <0, то d(lnm) <0 – вещество уходит из жидкой фазы. Физический смысл здесь ясен. Если dt >0, количество жидкости увеличивается, а если dt <0 – уменьшается. Если i = 1, т. е. компонент легколетучий, имеем

y1 > x1 dt >0, то dx1 >0 или

y1 < x1 dt <0, то dx1 <0

Таким образом, для легколетучего компонента, согласно физическому смыслу, если уходит dm молей состава пара, то уменьшается концентрация компонента 1 в жидкости, а если приходит – увеличивается.

Если же i = 2, то y2 < x2, dt <0, dx2 >0

y2 < x2, dt >0, dx2 <0

Для тяжелолетучего компонента, если уходит dm состава пара, то концентрация компонента 2 в жидкости увеличивается, а если приходит – уменьшается.

Вместе с тем, вектор направлен противоположно вектору-ноде , если dm молей уходит из жидкости и имеет то же направление, если dm молей приходит в жидкую фазу. Это видно из уравнения

3.4

В обоих случаях векторы колинеарны, это значит лежат на одной прямой, а их знаки определяются знаком dt как скалярного множителя (бесконечно малого).

Делаем вывод, что на диаграмме (рис. 3.1) в случае постоянной температуры и переменного давления вектор лежит на одной прямой с вектором, который имеет координаты . Если же рассматривается этот же состав x1, имеющий объем Vж, то при постоянном давлении и температуре направление вектора должно совпадать с направлением изотермо-изобары жидкой фазы. Следовательно, этот вектор не колинеарен вектору <Vп – Vж, y1 – x1>. Образно говоря, движущая сила этого смещения состава другая. Эта движущая сила должна лежать на касательной к изотермо-изобаре жидкости, то есть, проекция на ось абсцисс x, y остается при этом неизменной, а изменяется проекция на ось ординат V. Таким образом, векторы и имеют разное направление, то есть, смещены друг относительно друга на угол .

Величина, определяющая вектор , находится по определенной методике.

1. Проводим касательную к изотермо-изобаре жидкости в точке x1, Vж.

2. Пересечение касательной с прямой y1 = const дает вторую точку вектора

(т. А).

Получаем вектор .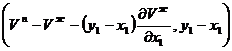

Начальной точкой этого вектора является точка с координатами (x1, Vж). Конечной точкой является точка А. Если рассматривается нода жидкость-пар, то ее координаты (Vп-Vж, y1-x1). Таким образом, имеем до точки азеотропа:

Vп-Vж > 0, y1-x1 > 0, > 0