Результаты одного лабораторного периодического опыта в принципе позволяют определить кинетическую функцию . В действительности нужно провести серию опытов в диапазоне интересующих значений концентрации активного реагента и температуры. Это необходимо для обеспечения надежности кинетических величин.

Кроме того, проведение серии опытов необходимо для экспериментального подтверждения инвариантности кинетической функции относительно концентрации и температуры.

Результатом такой серии опытов будет совокупность кривых . Из каждой кривой нужно определить кинетическую функцию, вычислив для ряда значений соответствующие значения х по формуле (18). Из этой формулы следует, что для расчета нужно знать время полного растворения в периодическом опыте и иметь достаточно надежные данные о ходе кинетической кривой во всем диапазоне значений от 0 до .

Аргумент кинетической функции х есть отношение продолжительности растворения и времени полного растворения . Величина играет, следовательно, роль нормировочного множителя или масштабного коэффициента, позволяющего выразить время в безразмерных единицах. В качестве такого коэффициента с равным успехом может быть использовано время, необходимое для достижения любого фиксированного значения . Пусть это фиксированное значение равно , оно должно быть выбрано таким образом, чтобы изменению от 1 до соответствовали достаточно надежные участки всех экспериментальных кривых. Время, необходимое для достижения значения при постоянных температуре и концентрации активного реагента, обозначим через . Введем теперь новое безразмерное время : 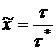. При обработке экспериментальных данных относящихся к каждому проведенному опыту, вместо определения х по формуле (18) вычисляют значения по формуле:

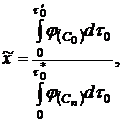(25)

где -время, необходимое для достижения в периодическом опыте.

В результате такой обработки экспериментальных данных получают зависимость доли нерастворившегося компонента от безразмерного времени

при постоянных концентрации активного реагента и температуре. Нетрудно убедиться в том, что, зависимость есть полный аналог кинетической функции . Аргументы х и отличаются друг от друга лишь постоянным множителем.

Действительно, из соотношени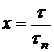й и 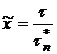следует, что

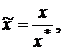(26)

где 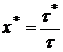- значение безразмерного времени х, отвечающее выбранной фиксированной величине . Соотношение (26) показывает, что зависимость сохраняет присущее кинетической функции свойство инвариантности относительно условий проведения процесса (поскольку величины х и не зависят от этих условий).

Переход от функции к кинетической функции эквивалентен простому изменению масштаба по оси абцисс. Это поясняется рисунком 2, где обе зависимости и - изображаються одной и той же кривой и различаются только масштабом по оси абцисс. В отличие от х, изменяющегося от 0 до 1, аргумент зависимости изменяется от 0 до некоторого значения .