2. По уравнению (18) вычисляют значение х, отвечающее определенному значению .

При этом верхний предел интеграла, стоящий в числителе, означает время необходимое для достижения этого значения в периодическом опыте. Такие вычисления проводят для ряда последовательных значений доли нерастворившегося компонента . Результаты расчетов, представленные в виде графика, таблицы или апроксимированные аналитическим выражением, дают кинетическую функцию

Графический вариант описанного метода иллюстрируется рис.1

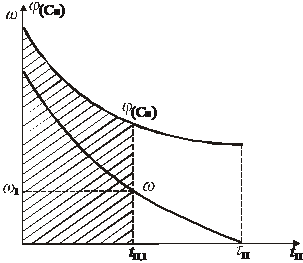
Рис.1. К графическому определению кинетической функции

Значение х соответствующее некоторому , равно отношению заштрихованной площади ко всей площади под кривой . С помощью такого графика можно легко определить значение х для ряда значений и составить таблицу или построить график зависимости .

Из уравнения (18) видно, что для определения х нужно знать зависимость скорости процесса от концентрации, т.е. функцию .

Если, например , то должен быть известен порядок реакции . Тогда уравнение (18) принимает вид:

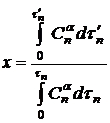(19)

Входящие в уравнение (18) и (19) интегралы могут быть определены численными или графическими методами. Необходимая для выполнения интегрирования зависимость от , а также связь между и , содержатся в результатах периодического опыта.

Таким образом, уравнение (18) позволяет вычислить значения, отвечающие любому значению , и тем самым определить кинетическую функцию.