Для мономолекулярных обратимых реакций типа А « В дифференциальные формы кинетического уравнения:

,(6.1)

.(6.2)

При равновесии 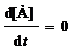, и если при t = 0 [B] = 0, то

[В]р/[А]рКр; (6.3)

[B]р = [А]0 - [А]р;(6.4)

[В]р [А]0,(6.5)

где [А], [B] – текущие концентрации веществ А и В; [А]0 – концентрация А при t = 0; k1 и k2 – константы скорости прямой и обратной реакций; [А]р и [B]р – концентрации А и В при равновесии; Кр– константа равновесия.

Интегральные формы кинетического уравнения:

;(6.6)

. (6.6а)

При условии, что в момент времени t = 0 [B]0 = 0:

.(6.7)

Для мономолекулярных параллельных реакций типа

С ¬ А ® В дифференциальные формы кинетического уравнения:

;(6.8)

.(6.9)

Интегральные формы кинетического уравнения:

; (6.10)

, (6.11)

где k1 и k2 – константы скорости первой и второй реакций. Константы скоростей отдельных стадий для реакций данного типа определяют по соотношению:

х1/х2 = k1/k2, (6.12)

где х1 и х2 – количества молей веществ В и С, образовавшихся к моменту времени t или приращение концентраций веществ В и С. Текущая концентрация исходного вещества имеет вид

[А] = [А]0 – х. (6.12а)

Для мономолекулярных последовательных реакций типа

дифференциальные формы кинетического уравнения:

; (6.13)

; (6.14)

; (6.15)

; (6.16)

. (6.17)

Интегральные формы кинетического уравнения:

; (6.18)

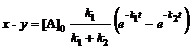; (6.19)

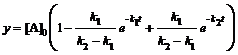; (6.20)

; (6.21)

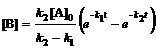; (6.22)

[C] = [А]0 - [А] - [B], (6.23)

где [А], [В], [С] – текущие концентрации веществ А, В, С; [А]0 – концентрация вещества А при t = 0; k1 и k2 – константы скорости первой и второй реакций: [А] = [А]0 – х; [В] = x – y; [C] = y.

Точка максимума на кривой [В] = f(t) характеризуется уравнениями

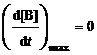; (6.24)

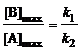; (6.25)

, (6.26)

где tmax – время соответствующее максимальной концентрации вещества В.