Как следует из экспериментальных данных по системе никель-кремний (рис.1.1), никель-кислород (рис.1.3) и кремний-кислород (рис.1.4) схема фазовых равновесий в системе никель-кремний-кислород при 298 К и 1 атм. имеет вид (рис.2.2).

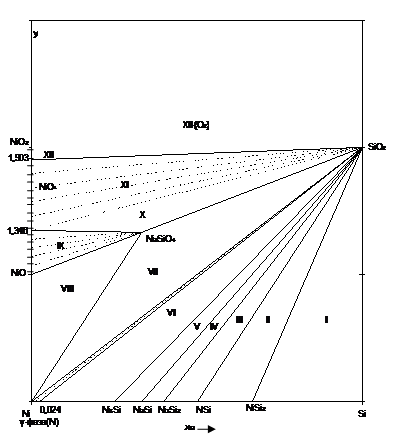
Рис.2.2 Фазовая диаграмма состояния системы Ni-Si-O при 25 0С.

Поскольку химическое сродство кремния к кислороду выше, чем никеля, то можно предположить, что почти при любом составе сплава Ni-Si в первую очередь будет реализовываться равновесие сплав - SiO2.

На диаграмме 2.2 можно выделить области, в которых присутствуют следующие фазы:

1. Si (γ) - NiSi2 - SiO2; (I)

2. NiSi2 - NiSi - SiO2; (II)

3. NiSi - Ni3Si2 - SiO2; (III)

4. Ni3Si2 - Ni2Si - SiO2; (IV)

5. Ni2Si - Ni3Si - SiO2; (V)

6. Ni3Si - γ-фаза - SiO2; (VI)

7. γ - фаза - Ni2SiO4 - NiO; (VII)

8. γ-фаза - Ni2SiO4 - NiO; (VIII)

9. Ni2SiO4 - NiOх, 1<x<1,346; (IX)

10. Ni2SiO4 - SiO2 - NiOx, 1,346<x<1,903; (XI)

Примеры расчета:

а) Фазовое равновесие VII:

γ-фаза - Ni2SiO4 - SiO2 было описано независимыми реакциями образования SiO2 и Ni2SiO4 из компонентов γ-фазы (Ni, Si) и компонентов газовой фазы O2:

(1) ;

(2) ;

Константы равновесия реакций 1 и 2:

; (2.3), ; (2.4)

Для определения состава γ-фазы исключим из конечного термодинамического уравнения. Для этого возведем уравнение (2.3) в квадрат и поделим полученное на уравнение (2.4), получим:

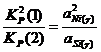; (2.5)

Это уравнение можно переписать в виде:

; (2.6)

Из уравнения изотермы химической реакции:

; (2.7)

уравнение (2.3.4) можно переписать:

; (2.8)

Данное трансцендентное уравнение можно решить только численным методом. Обозначив xSi=x, xNi=x-1, получим:

; (2.9)

; (2.10)

Подставив уравнения (2.9) и (2.10) в (2.8) решаем численным методом, находим значение х. Исходя из уравнений (2.3) или (2.4) определяем величину .

Для остальных трехфазных равновесий расчет производился тоже исходя из константы равновесия. Например, для равновесия IV:

Мольные доли компонентов равны единице, поэтому выражение для константы равновесия упрощается:

; (2.11)

Результаты расчетов приведены в таблице 2.5.

Таблица 2.5.

Характеристики фазовых равновесий системы Ni-Si-O при 25 0С