Рассчитайте случайную ошибку определения серы в стали, если в ходе анализа были получены следующие данные: 0,0123; 0,0125; 0,0121; 0,0123; 0,0122 % S
Дипломы, курсовые и прочее / Методы контроля и анализа веществ (химические методы) / Дипломы, курсовые и прочее / Методы контроля и анализа веществ (химические методы) / Рассчитайте случайную ошибку определения серы в стали, если в ходе анализа были получены следующие данные: 0,0123; 0,0125; 0,0121; 0,0123; 0,0122 % S Рассчитайте случайную ошибку определения серы в стали, если в ходе анализа были получены следующие данные: 0,0123; 0,0125; 0,0121; 0,0123; 0,0122 % S

Решение:

Наличие грубых ошибок (промахов) оцениваем по Q-критерию. Располагаем экспериментальные данные в порядке возрастания величин 0,0121, 0,0122, 0,0123, 0,0123, 0,0125.

Предполагаем, что значения 0,0121 и 0,0125 являются результатом случайной ошибки.

Рассчитаем критерий Q для этих величин по формуле

где – размах варьирования – разница между двумя крайними значениями в ряду величин (расположенных в порядке возрастания) – подозрительно выделяющееся значение; – соседнее с ним значение.

Для и табличное значение . и , поэтому грубая ошибка в измерениях 0,0121 и 0,0125 отсутствует.

Находим стандартное отклонение:

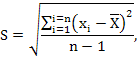
где – единичное отклонение, т. е. отклонение отдельного измерения от среднего арифметического; – число степеней свободы.

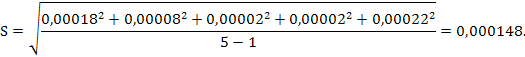
Стандартное отклонение среднего результата равно:

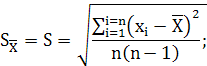
Вычисляем доверительный интервал, принимая

;

Оцениваем еще раз наличие случайных ошибок по критерию :

Сравнивая величины и , видим, что ни одно из отклонений от среднего не выходит за пределы . Следовательно величины не содержат грубых ошибок.

Так как выборка не содержит грубых ошибок то ее можно обрабатывать с применением методов математической статистики.

Тогда, интервал, в котором с вероятностью лежит истинное значение, равен

т. е. % S – это и есть оценка случайной ошибки.

Смотрите также

История открытия и подтверждения периодического закона Д.И. Менделеева
Периодический закон Д.И. Менделеева – это фундаментальный закон, устанавливающий периодическое изменение свойств химических элементов в зависимости от увеличения зарядов ядер их атомов ...

Физико-химические закономерности получения полиамидов (полиамид-6, полиамид-6,6, полиамид-10)
Полиамиды представляют огромный по числу представителей и очень важный по своему научному и практическому значению класс высокомолекулярных соединений. Почти полтора века, которые прошли ...

Применение органических реагентов в аналитической химии
Органические вещества широко применяются в аналитической химии вообще и в фармацевтическом анализе, в частности. Ещё с начала нашей эры было известно, что настой чернильных дубильных орешко ...