Вт/мК

Тогда

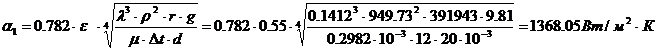
Тогда поверхностная плотность теплового потока первой стенки определим по формуле:

Примем, что

Определим температуру второй стенки по формуле:

Определим коэффициент теплопроводности для воды при t=29.32 ْC с помощью интерполяции справочных данных:

Аналогично определим коэффициент теплопроводности для воды при t=32.5 ْC:

Определим вязкость жидкости для воды при t=29.32 ْC с помощью интерполяции справочных данных:

Па

Аналогично определим вязкость воды при t=32.5 ْC:

Па

Определим теплоемкость воды t=29.32 ْC с помощью интерполяции справочных данных:

Аналогично определим теплоемкость воды при t=32.5 ْC:

Определим критерий Рейнольдса по формуле:

,

где - вязкость смеси, Па.с;

G- расход воды, кг/с;

z- число ходов, z=4;

d- внутренний диаметр труб, м;

Nтр- количество труб.

Определим критерий Прандтля для потока и стенки при температурах tср=29.32ْС, tст=32.5ْС:

,

где с- теплоемкость воды, Дж/кгК;

теплопроводность воды, Вт/(м.К);

-вязкость воды, мПа.с.

Определим критерий Нуссельта по формуле:

Зная критерий Нуссельта, определим коэффициент теплоотдачи второй стенки по формуле:

Тогда

Тогда поверхностная плотность теплового потока первой стенки определим по формуле:

Сопоставим q1 и q2, т разность выразим в процентах:

Выбранная температура стенки наугад не подходит.

3. Используя графический метод, определяем температуру стенки в третьем приближение-

ْC (графическое решение приведено в приложение 5).

Проводим расчеты аналогичные расчетам, выполненным в пункте 2.