Меню сайта
Наши новости
Распространение алкалоидов в растительном мире.
Умягчение воды
Уточнённый расчёт поверхности теплопередачи. Второе
приближениеДипломы, курсовые и прочее / Расчёт многокорпусной выпарной установки / Дипломы, курсовые и прочее / Расчёт многокорпусной выпарной установки / Уточнённый расчёт поверхности теплопередачи. Второе
приближение Уточнённый расчёт поверхности теплопередачи. Второе
приближениеСтраница 2
![]() град
град
![]() град
град
Для расчета коэффициента теплопередачи α2 физические свойства кипящих растворов Na2SO4 и их паров приведены в таблице 7.
![]()
![]() Вт/(м2∙К)
Вт/(м2∙К)
Проверим правильность первого приближения по равенству удельных тепловых нагрузок:
![]() Вт/м2
Вт/м2
![]() Вт/м2
Вт/м2
Как видим, q’ ≠ q”. Для второго приближения примем Δt1 = 4 град, пренебрегая изменением физических свойств конденсата при изменении температуры, рассчитываем α1 по соотношению:
Таблица 7. Физические свойства кипящих растворов Na2SO4 и их паров
|
Параметр |
Корпус | ||
|
1 |
2 |
3 | |
|
Теплопроводность раствора λ, Вт/(м∙К) |
0,344 |
0,352 |
0,378 |
|
Плотность раствора ρ, кг/м3 |
1071 |
1117 |
1328 |
|
Теплоёмкость раствора с, Дж/(кг∙К) |
3876 |
3750 |
3205 |
|
Вязкость раствора μ, Па∙с |
0,26 |
0,3 |
0,6 |
|
Поверхностное натяжение σ, Н/м |
0,0766 |
0,0778 |
0,0823 |
|
Теплота парообразования rв, Дж/кг |
2197∙ 103 |
2219∙ 103 |
2268∙ 103 |
|
Плотность пара ρп, кг/м3 |
1,19 |
0,914 |
0,514 |
![]() Вт/(м2∙К)
Вт/(м2∙К)
Тогда получим:
![]() град
град
![]() град
град
![]() Вт/(м2∙К)
Вт/(м2∙К)
![]() Вт/м2
Вт/м2
![]() Вт/м2
Вт/м2
Очевидно, что q’ ≠ q”. Для расчёта в третьем приближении строим графическую зависимость удельной тепловой нагрузки q от разности температур между паром и стенкой (рис. 4) и определяем Δt1.
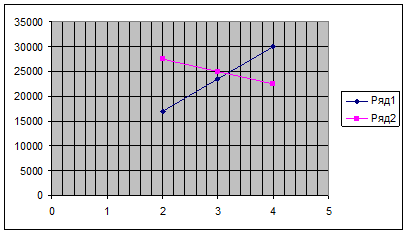
Рис. 4. График зависимости удельной тепловой нагрузки q от разности температур Δt1
Согласно графику можно определить Δt1 = 3,2 град. Отсюда получим:
![]() Вт/(м2∙К)
Вт/(м2∙К)
![]() град
град
![]() град
град
![]() Вт/(м2∙К)
Вт/(м2∙К)
![]() Вт/м2
Вт/м2
![]() Вт/м2
Вт/м2
Как видим, q’ ≈ q”. Так как расхождение между тепловыми нагрузками не превышает 3%, на этом расчёт коэффициентов α1 и α2 заканчиваем и находим К1:
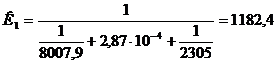 Вт/(м2∙К)
Вт/(м2∙К)
Далее рассчитываем коэффициент теплопередачи для второго корпуса К2. Примем в первом приближении Δt1 = 2,0 град. Для определения К2 найдём:
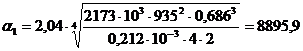 Вт/(м2∙К)
Вт/(м2∙К)
![]() град
град
![]() град
град
![]()
![]() Вт/(м2∙К)
Вт/(м2∙К)
![]() Вт/м2
Вт/м2
Смотрите также
Энтальпия и ее отношение к теплоте химической реакции. Типы химических связей
...
Исследование расщепления крахмала под действием a-амилазы слюны
Амилазы
широко используются в пищевой промышленности. Так амилазы используются в
хлебопечении и технологиях брожения. Также a-амилаза
играет значительную роль в расщеплении крахмала в орган ...
Дериватография
Комплексный метод
исследования химических и физико-химических процессов, происходящих в образце в
условиях программированного изменения температуры. Основан на сочетании
дифференциального термическ ...


