Для нахождения векторов стехиометрических чисел ,т.е. матрицы Г, решается система уравнений

(9)

Для решения системы (9) используем только линейно-независимые столбцы матрицы ВХ

и один вектор из матрицы Г

. Например, для двухмаршрутного каталитического процесса с катализатором М и первым интермедиатом Х1 имеем матрицу ВХ(rank BX

= 2) S = 4 и вектор .

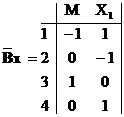
Получим 2 уравнения:

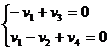(10)

Для решения системы двух уравнений с четырьмя неизвестными разделим переменные на независимые, значения которых задаём, и зависимые

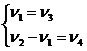. (11)

При таком разделении системы уравнений следует проверить, чтобы определитель левой части D ≠ 0, иначе система не будет иметь решения. Для удобства нахождения значений ν1 и ν2 (при заданных ν3 и ν4), систему (11) приводят к единичному базису (метод Жордано-Гаусса) так, чтобы каждое уравнение слева имело одно неизвестное. Так, сложив уравнения в системе (11), получим ν2 = ν3 + ν4 и система (11) примет вид 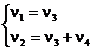(12)

(12)

Задавая ν3 = 1 и ν4 = 0, получим ν1 = 1 и ν2 = 1, т.е. для первого маршрута. При ν3 = 0 и ν4 = 1 ν1 = 0 и ν2 = 1 и для второго маршрута. При ν3 = 0 и ν4 = 0 все решения будут нулевыми.

Пример 2. Рассмотрим пример нелинейного механизма.

(13)

Здесь одно линейно-независимое промежуточное соединение Х (NI = 1), 2 стадии (S = 2) и один маршрут Р = 2 – 1 = 1. Матрицу стехиометрических коэффициентов интермедиатов ВХ

запишем вектором-строкой . Поскольку , умножим вектор-строку на вектор столбец . Получим одно уравнение

ν1 – 2ν2 = 0, (14)

которое имеет одно линейно-независимое решение. Задав ν1 = 1, получим ν2 = 0.5. При ν1 = 2 ν2 = 1 и т.д. Если при сложении стадий (1) и (2) (для исключения Х из итогового уравнения) умножим стадии (1) и (2) на наборы |1 0.5| или |2 1|, получим итоговые уравнения, соответственно, маршрутов N(1) и N(2):

N(1) А = 1/2 Р

N(2) 2А = Р

Очевидно, что ΔG(Р) (по маршруту N(Р)) определяется уравнением (15)

(15)

В соответствии с уравнением (7) для ΔG(Р) и для ΔGj получаем:

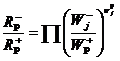(16)

где –скорости элементарной стадии в прямом и обратном направлениях.

Для маршрута N(1):

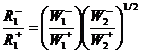(17)

Для маршрута N(2):

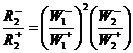(18)