Меню сайта
Наши новости
Распространение алкалоидов в растительном мире.
Умягчение воды
Уравнение Клаузиуса — КлапейронаДипломы, курсовые и прочее / Фазовые равновесия / Дипломы, курсовые и прочее / Фазовые равновесия / Уравнение Клаузиуса — Клапейрона Уравнение Клаузиуса — КлапейронаСтраница 1
Клаузиус показал, как можно упростить уравнение Клапейрона для случаев испарения и возгонки, исходя из предположения, что пар подчиняется закону идеального газа и что мольным объемом жидкости ![]() (ж) по сравнению с мольным объемом пара
(ж) по сравнению с мольным объемом пара ![]() (пар) можно пренебречь. Например, для воды при 100° V(пар) =30.2 л а V(ж)=0,0188 л. Подставляя RT/Р вместо V (пар), получим
(пар) можно пренебречь. Например, для воды при 100° V(пар) =30.2 л а V(ж)=0,0188 л. Подставляя RT/Р вместо V (пар), получим
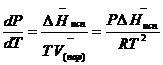 (28)
(28)
После преобразования выражение принимает вид:
![]() (29)
(29)
![]() (30)
(30)
Интегрирование в предположении, что ![]() не зависит от температуры, дает:
не зависит от температуры, дает:
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
где С — константа интегрирования.
Теперь очевидна теоретическая основа эмпирического соотношения ![]() . Уравнение (32) представляет собой уравнение прямой линии, если рассматривать lnР как функцию
. Уравнение (32) представляет собой уравнение прямой линии, если рассматривать lnР как функцию ![]() . Тангенс угла наклона прямой равен
. Тангенс угла наклона прямой равен ![]() а при использовании десятичных логарифмов он равен
а при использовании десятичных логарифмов он равен ![]() . Таким образом, теплоту испарения можно рассчитать с применением выражения
. Таким образом, теплоту испарения можно рассчитать с применением выражения
![]()
![]()
![]()
![]() (34)
(34)
Часто удобнее пользоваться уравнением, полученным при интегрировании в пределах Р2, Т2 и Р1, Т1:
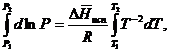 (35)
(35)
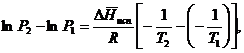 (36)
(36)
![]() (37)
(37)
По этому уравнению можно рассчитать теплоту испарения, исходя из давления равновесного пара при двух различных температурах; если известны теплота испарения и давление пара при одной температуре, можно рассчитать давление пара при другой температуре при условии, что ![]() остается постоянной. Давление можно выразить в любых единицах, но эти единицы должны быть одинаковыми для обоих давлений. Точно так же можно выбрать любые единицы энергии при условии, что
остается постоянной. Давление можно выразить в любых единицах, но эти единицы должны быть одинаковыми для обоих давлений. Точно так же можно выбрать любые единицы энергии при условии, что![]() и R будут выражены в одинаковых единицах. Изменение давления пара твердого вещества с температурой можно выразить с помощью уравнения (37) при условии, что температурный интервал не слишком широк. Вследствие того, что теплота возгонки твердого вещества больше, чем теплота испарения соответствующей жидкости, давление пара твердого вещества быстрее изменяется с температурой, чем давление пара соответствующей жидкости, и кривая идет круче. Дифференциальное выражение (28) можно применять, если изменения температуры и давления малы. Например, удобно пользоваться следующей формулой для внесения поправок в температуру кипения при колебаниях атмосферного давления:
и R будут выражены в одинаковых единицах. Изменение давления пара твердого вещества с температурой можно выразить с помощью уравнения (37) при условии, что температурный интервал не слишком широк. Вследствие того, что теплота возгонки твердого вещества больше, чем теплота испарения соответствующей жидкости, давление пара твердого вещества быстрее изменяется с температурой, чем давление пара соответствующей жидкости, и кривая идет круче. Дифференциальное выражение (28) можно применять, если изменения температуры и давления малы. Например, удобно пользоваться следующей формулой для внесения поправок в температуру кипения при колебаниях атмосферного давления:
![]() (38)
(38)
Так как уравнение (37) для расчета теплоты испарения выведено в предположении, что пар есть идеальный газ, то результаты, получаемые при пользовании этим уравнением, не более точны, чем расчеты, в которые входит уравнение ![]() .
.
Другое приближение содержит допущение о том, что теплота испарения не зависит от температуры. Однако в широком интервале температур графики зависимости lgP от 1/Т несколько искривлены, потому что ![]() меняется с температурой. В этом случае можно рассчитать теплоту испарения для какой-нибудь определенной температуры из наклона кривой путем проведения касательной к этой кривой при заданной температуре. Уравнение для давления равновесного пара, которое дает линейное изменение
меняется с температурой. В этом случае можно рассчитать теплоту испарения для какой-нибудь определенной температуры из наклона кривой путем проведения касательной к этой кривой при заданной температуре. Уравнение для давления равновесного пара, которое дает линейное изменение ![]() с температурой, можно вывести следующим образом. Согласно уравнению
с температурой, можно вывести следующим образом. Согласно уравнению ![]() зависимость мольной теплоты испарения
зависимость мольной теплоты испарения ![]() от температуры выражается уравнением
от температуры выражается уравнением
Смотрите также
Заключение
В процессе
проделанной работы была рассчитана ректификационная колонна для разделения
смеси бензол–толуол.
В
результате расчета получены данные:
1) &nbs ...
Реакции спиртов. Кислотно-основные свойства спиртов. Реакции с участием нуклеофильного центра
Спирты представляют собой соединения
общей формулы ROH, в которых гидроксильная группа присоединена к насыщенному
атому углерода. По номенклатуре ИЮПАК насыщенные спирты называют алканолами, ...
Тонкослойная хроматография и ее роль в контроле качества пищевых продуктов
Хроматография,
обязательно включающая процесс разделения смесей веществ в динамическом режиме,
охватывает не только достаточно обширный раздел аналитической химии, но и лежит
в основе ряда ...


