Меню сайта
Наши новости
Распространение алкалоидов в растительном мире.
Умягчение воды
Уравнение КлапейронаДипломы, курсовые и прочее / Фазовые равновесия / Дипломы, курсовые и прочее / Фазовые равновесия / Уравнение Клапейрона Уравнение Клапейрона
Термодинамическое обоснование эмпирических соотношений между давлением равновесного пара и температуре было дано Клапейроном в 1834 г. Рассмотрим жидкость, находящуюся в равновесии с ее паром при температуре Т и давлении, равном давлении равновесного пара Р при этой температуре.
Термодинамическим критерием равновесия при постоянных температуре и давлении является равенство изобарных потенциалов для этих двух состояний:
![]() , (16)
, (16)
где «ж» и «пар» — индексы, обозначающие жидкость и пар.
Если температура повысилась до Т+dТ, то для того чтобы обе фазы остались в равновесии, давление должно увеличиться до Р+dР, равного давлению пара при этой более высокой температуре. При бесконечно малом повышении температуры и давления изобарный потенциал для жидкости станет равным G(ж)+dG(ж), а для пара G(пар)+dG(пар). Так как обе фазы находятся в равновесии, то
![]() (17)
(17)
С учетом уравнения (16) условие сохранения равновесия при изменении температуры и давления имеет вид:
![]() (18)
(18)
Так как dG представляет собой полный дифференциал, то уравнение (18) можно написать следующим образом:
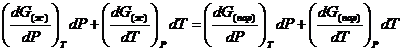 (19)
(19)
На основании уравнений ![]() и
и ![]() уравнение (19) можно переписать в виде
уравнение (19) можно переписать в виде
![]() (20)
(20)
При подстановке получим
![]() (21)
(21)
Так как по уравнению
![]()
![]()
![]() (22)
(22)
где ![]() — изменение энтальпии при испарении жидкости при температуре Т, то уравнение (21) можно написать следующим образом:
— изменение энтальпии при испарении жидкости при температуре Т, то уравнение (21) можно написать следующим образом:
![]() (23)
(23)
Это важное соотношение известно как уравнение Клапейрона. Оно дает зависимость скорости изменения давления равновесного пара с температурой (dР/dТ) от энтальпии испарения ![]() , объема жидкости V (ж) и объема пара V(пар) при температуре Т и давлении, равном давлению насыщенного пара. Вследствие того что вывод уравнения (23) не зависит от каких-либо предположений относительно природы обеих фаз, можно легко вывести такие же уравнения для равновесия между твердым веществом и паром, находящимся в равновесии с ним, а также для равновесия между твердым веществом и жидкостью и между двумя различными кристаллическими формами твердого вещества. Для этих случаев уравнение (23) можно написать так:
, объема жидкости V (ж) и объема пара V(пар) при температуре Т и давлении, равном давлению насыщенного пара. Вследствие того что вывод уравнения (23) не зависит от каких-либо предположений относительно природы обеих фаз, можно легко вывести такие же уравнения для равновесия между твердым веществом и паром, находящимся в равновесии с ним, а также для равновесия между твердым веществом и жидкостью и между двумя различными кристаллическими формами твердого вещества. Для этих случаев уравнение (23) можно написать так:
![]() (24)
(24)
![]()
![]() (25)
(25)
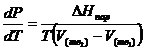 (26)
(26)
где ![]() ,
, ![]() и
и ![]() — энтальпии возгонки, плавления и перехода (между твердым состоянием 1 и 2) соответственно. Теплоты возгонки, плавления и испарения при заданной температуре связаны соотношением
— энтальпии возгонки, плавления и перехода (между твердым состоянием 1 и 2) соответственно. Теплоты возгонки, плавления и испарения при заданной температуре связаны соотношением
![]() (27)
(27)
поскольку количество тепла, необходимое для испарения данного количества твердого вещества, остается постоянным, независимо от того, проводится ли процесс испарения твердого вещества непосредственно или путем первоначального плавления твердого вещества с последующим испарением жидкости. Каждое из этих уравнений можно выразить через мольные величины.
При пользовании уравнениями (23) — (26) необходимо выражать изменение энтальпии процесса в тех же единицах, что и произведение давления на изменение объема. Для этой цели полезно рассчитать множитель для перевода кал в л • атм:
![]()
Смотрите также
Получение платины из стоков процесса рафинирования металлов платиновой группы
В ходе работ по
выделению ценных элементов из стоков процесса рафинации платиновых металлов
было установлено, что все возможные методы, дающие отличные результаты при
использовании синтетич ...


