В равновесной системе связь между числами фаз, компонентов и термодинамических степеней свободы выражается правилом фаз Гиббса или законом равновесия фаз. Рассмотрим равновесную термодинамическую систему, состоящую из Ф фаз, каждая из которых содержит К компонентов. Примем в качестве параметров, определяющих состояние системы, давление, температуру и концентрации компонентов, выраженные в массовых или молярных долях или процентах. Оценим общее число параметров состояния и число уравнений, связывающих их. Число параметров, одинаковых во всех фазах системы, равно двум (Р и Т). Поскольку концентрации компонентов выражены в массовых или молярных долях или процентах, то для характеристики состава одной фазы достаточно задать (К — 1) концентраций. Концентрация одного из компонентов данной фазы будет определена, если известны концентрации остальных компонентов. Для характеристики состава всех фаз равновесной системы необходимо знать Ф(К — 1) концентраций. Тогда общее число параметров, определяющих состояние равновесной системы, будет равно Ф(К — 1) + 2.

Так как при Р = соnst T=const химические потенциалы компонентов являются функциями их концентраций, например, в идеальном растворе, то число уравнений, связывающих концентрации компонентов равновесной системы, можно определить из равенства химических потенциалов каждого компонента во всех фазах :

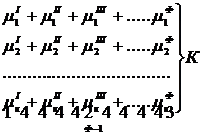(1)

Число уравнений, связывающих концентрации одного компонента, равно (Ф — 1), а всех К компонентов — К(Ф — 1). Число независимых параметров состояния системы, т.е. число термодинамических степеней свободы, равно разности между общим числом параметров, определяющих состояние равновесной системы, и числом уравнений, связывающих эти параметры:

С = Ф(К - 1) + 2 - К(Ф - 1),

С=К-Ф + 2. (2)

Уравнение (2) называется правилом фаз Гиббса

или законом равновесия фаз

: в равновесной термодинамической системе, на которую из внешних факторов оказывают влияние только давление и температура. Число термодинамических степеней свободы равно числу компонентов минус число фаз плюс два. Число степеней свободы возрастает с увеличением числа компонентов и уменьшается с увеличением числа фаз. Поскольку число степеней свободы не может быть отрицательным, число фаз в равновесной системе не может превышать К + 2.

Правило фаз было выведено американским физиком Дж. Гиббсом в 1876 г. Учение о фазах в дальнейшем было использовано в работах Я. Вант-Гоффа, Б. Розебома, Н.С. Курнакова и др. и явилось основой изучения равновесий в гетерогенных системах. Если из внешних факторов на систему оказывает влияние только давление (Р=соnst) или температура (T=const), число степеней свободы уменьшается на единицу и уравнение правила фаз (2) принимает вид

СуСЛ = К-Ф+1 (3)

Вариантность системы, рассчитанная по этому уравнению, называется условной (Сусл), а система — условно инвариантной, условно моновариантной и т.д. При постоянстве давления и температуры

Cусл=К-Ф (4)

Если составы двух равновесных фаз, например жидкой и парообразной, одинаковы, то при подсчете числа степеней свободы следует учитывать еще одно уравнение, связывающее концентрации компонентов Х,(ж) = Х,(п). В этом случае вместо уравнения (2) следует пользоваться уравнением

СуСЛ =

К-Ф+1 (5)

а вместо уравнения (3) — уравнением

Cусл=К-Ф

(6)

Если состояние системы определяется и такими внешними факторами, как электрическое или магнитное поле, поле тяготения и др., то их также следует учитывать при подсчете числа степеней свободы в равновесной системе. В общем случае, когда на систему действуют п различных факторов, то

С=К-Ф+n (7)