Первичная обработка результатов исследования химического равновесия основана на рекомендациях [38, 101-104] и включала в себя следующее.

Расчет отношений концентраций компонентов, характеризующих константы равновесия изучаемых реакций.

Анализ изученных отношений с целью установления момента достижения равновесия и включения в обработку только равновесных данных.

2. Исключение грубых ошибок внутри серии определений константы равновесия. Для каждой температуры исследования сериями считали опыты, различающиеся между собой либо составом исходной смеси, либо количеством катализатора. Отбраковку промахов в сериях проводили с использованием критерия – наибольшего по абсолютной величине нормированного выборочного отклонения:

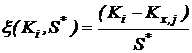,где - значение константы равновесия; - среднее арифметическое значение константы равновесия в серии j; 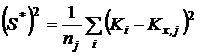- смещенная дисперсия ; - число результативных определений константы равновесия в серии j.

Процентные точки наибольшего по абсолютной величине нормированного выборочного отклонения заимствованы из работы [102].

3. Расчет среднего арифметического значения константы равновесия и дисперсии воспроизводимости в сериях после исключения грубых ошибок:

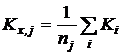
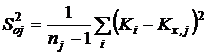
Сопоставление дисперсий воспроизводимости констант равновесия в сериях при одной температуре. Эта стадия дисперсионного анализа является весьма полезной, так как позволяет контролировать ошибки воспроизводимости, возникающие на всех этапах получения экспериментальной информации. Проверку равенства дисперсий воспроизводимости в сериях выполняли по двум критериям: Фишера – если число серий равнялось двум и Бартлетта – когда количество серий превышало два [38, 102]. Если нуль-гипотеза выполнялась, то дисперсию воспроизводимости вычисляли по следующей формуле:

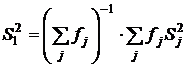, где .

Для всех изученных в данной работе превращений дисперсии воспроизводимости констант равновесия в сериях были однородны.

Расчет среднего значения константы равновесия для каждой температуры исследования:

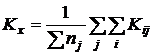
Проверку значимости расхождения средних значений констант равновесия в сериях. Для этого вычисляли дисперсию :

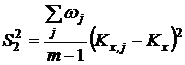
где m – число серий, wj – вес серии j, равный числу определений nj.

Величина характеризовала рассеяние значений относительно . Число степеней свободы дисперсии равнялось . Проверку гипотезы равенства средних значений констант равновесия в сериях проводили с помощью распределения Фишера. Если нуль-гипотеза выполнялась, то вычисляли сводную дисперсию