Меню сайта
Наши новости
Распространение алкалоидов в растительном мире.
Умягчение воды
Электронные спектры поглощения. Электронные спектры
красителей и модель одномерного ящика.Учим химию / Молекулярные спектры / Учим химию / Молекулярные спектры / Электронные спектры поглощения. Электронные спектры
красителей и модель одномерного ящика. Электронные спектры поглощения. Электронные спектры
красителей и модель одномерного ящика.Страница 2
2) Нам предстоит:
– связать наблюдаемые длины волн или частоты поглощаемого излучения с абсолютными размерами молекул с помощью теоретической модели,
– вычислить усреднённую длину связи C¼C в цепи -сопряжения из имеющихся спектральных данных.
–сравнить результаты расчёта с экспериментальными данными.
3) Примем во внимание, что
– Атомы C и N являются соседями в Периодической системе. Экспериментальные длины связей с одинаковой кратностью, т.е. C-C и C-N, или C=C и C=N, или CºC и CºN примерно равны, и в расчётах будем считать их равными.
4) Максимально упростим вычисления. Для этого
– не будем разделять связи разной кратности в системе сопряжения. Пренебрежём малыми отличиями их длин, и введём усреднённую длину связи, обозначая её a.
5) Отметим, что
Простейшая теоретическая модель для одной частицы в квантовой механике это известная модель одномерного потенциального ящика, в которой уровни энергии зависят от линейной протяжённости системы.
5.1 Модель ящика используем для граничных -электронов, которые находятся на высшей занятой МО (ВЗМО).
5.2 С ВЗМО электрон в молекуле полиена совершает спектральный переход, на ближайшую низшую свободную МО (НСМО). Её также называют низшей вакантной МО (НВМО).
5.3 Примем, что область делокализации -электронов, в том числе и на граничной занятой МО охватывает не только всю систему сопряжения, но и простирается далее за неё (для простоты примем по половине связи). Вследствие принципа Гейзенберга электрон невозможно локализовать.
5.4 При спектральном возбуждении молекулы поглощается фотон, и за счёт поглощённой энергии один электрон совершает переход между граничными МО (-ВЗМО Û -НВМО).
5.5 Энергия перехода, а с нею длина волны, частота и волновое число поглощаемого излучения определяется разностью уровней DE этих двух граничных МО (ГМО).
5.6 Энергетические уровни ГМО необходимо выразить как функции от длины полиеновой цепи между двумя одинаковыми концевыми гетероциклическими азотсодержащими остатками в молекулах соединений в изучаемом ряду красителей.
6) Применим для этих красителей модель свободного электрона (ящика).
Цель эадачи состоит в том, чтобы проверить, насколько абсолютные уровни энергии электронов, “размазанных” на делокализованных- пи-МО в молекулах органических полиенов согласуются с моделью одномерного потенциального ящика.
Примечания: Введённые допущения дополняют теорию МОХ, и ей не противоречат. В простой теории МОХ не используются в явной форме структурные признаки, в том числе длины связей и размеры молекулы. В простой теории МОХ отсутствует физически конкретная шкала энергии. Единицей энергии является отвлечённый параметр - хюккелевский резонансный интеграл.
Первый шаг в расчёте - построение теоретической модели и выяснение схемы вычислений:
6.1) Правило квантования уровней ящика: 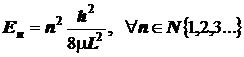 .
.
6.2) Номер граничного уровня -ВЗМО равен числу электронных пар – числу двойных связей. В кольцах и вне полиенового мостика это число равно 4 и в полиеновом мостике ещё k и всего получаем число -электронных пар (4+k), это же есть и номер ВЗМО(4+k) (см. структурную формулу). Номер m
уровня НВМО
, на которую при возбуждении переходит электрон, на 1 больше, и равен m
=
n
+1=4+k+1=5+k.
6.3) То же самое число (4+k) равно количеству чередующихся фрагментов с двойной и одинарной связью типа C
=
C
-
C
между двумя атомами N
.
Длина фрагмента N
+
=
C
-
C
(
или N
-
C
=
C
)
в циклах считается равной C
=
C
-
C
. Если усреднённая из-за сопряжения длина связи C
¼
C
равна
a
, то длина двух связей в звене цепи сопряжения равна 2a
,
и расстояние между атомами N
равно 2×(4+k) a
.
6.4) Учтём дополнительную протяжённость электронного облака за пределы системы сопряжения, добавляя к ней ещё одну длину связи. В таком случае длина ящика L
, в котором делокализован электрон, равна L
=
2(4+k)
a
+
a
= (9+2k)
a
.
6.5) Подытожим только что полученные расчётные формулы:
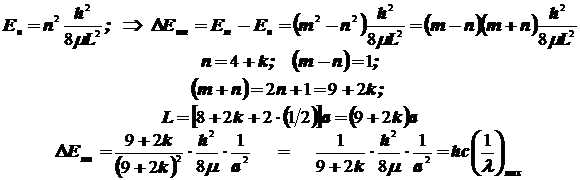
|
Смотрите также
Cложные эфиры
...
Фермент
Одним из фундаментальных понятий, как
биологии,так и химии является понятие “фермент”.Изучение ферментов имеет
большое значение для любой области биологии,а также для многих отраслей
химич ...