Энтропия
Страница 1

Наиболее информативной термодинамической функцией в уравне­нии (19) является энтропия S.

Значение энтропии легко определить только для состояния иде­ального газа. Используем для вычисления S уравнение (18), где dU — изменение внутренней энергии, равное для идеального газа СvdT т.е. теплоемкости при постоянном объеме, умноженной на приращение температуры: pdv — приращение работы, которое можно представить как, заменив р на RT/v. Отсюда Лучшие проститутки тулы ждут вашего звонка. | Шлюхи Наро-Фоминска гарантируют конфиденциальность и безопасность.

(20)

После интегрирования в пределах 0¾T получаем

(21)

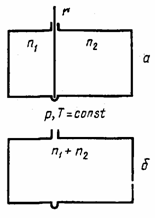
рис. 2 Схема для расчета энтропии при самопроизвольном смешивании двух газов.

где ST — энтропия при температуре Т; S0 — энтропийная постоян­ная; Сv — теплоемкость при постоянном объеме; v — молярный объем.

Таким образом, энтропия моля идеального газа является функцией Т и р (так как молярный объем зависит от Т и р). Выражение (21) применимо лишь для чистого идеального газа, так как для смесей газов, даже при отсутствии между ними химических реакций, энтропия смеси будет возрастать за счет необратимых процессов диффузии, приводящей к распределению компонентов по всему объему газовой смеси. Рассмотрим процесс самопроизвольного смешения двух газов.

Пусть в двух частях объема, разделенного перегородкой r (рис. 2, а), находится n1 молей первого газа и n2 молей второго газа при р, Т=const.

Общая энтропия системы

(22)

где S1 и S2 — молярные энтропии первого и второго газов. Удалим перегородку r и дадим возможность газам образовать смесь, равномерно распределенную по всему объему (рис 2,б), где v —молярный объем газа при данных р и Т. На каждый моль компонентов смеси приходятся пропорциональ­ные части объема:

и

Подставляем значения этих объемов в уравнение (21) и получаем значения энтропии для одного моля компонента в смеси:

Общий запас энтропии в смеси газов тоже увеличился:

(23)

Приращение энтропии в газовой смеси зависит от соотношения чисел молей компонентов n1 и n2. Если положить, что n1 → 0, то энтропия этого газа

но доля, вносимая этим компонентом в общий запас энтропии сис­темы, также стремится к нулю: . В то же время если n1→ 0, то (n1+n2)/n2 стремится к 1, а тоже стремится к нулю. Следовательно, при исчезновении одного из компонентов газовой смеси энтропия другого компонента станет равна энтропии чистого газа:

Страницы: 1 2 3

Смотрите также

Равновесие между жидкостью и паром
...

Синтез Na2O2 (пероксида натрия)
В повседневной жизни пероксиды очень важны для человека. Пероксид водорода, например, широко используется для отбеливания тканей и шерсти, соломы, перьев. Разлагая красящие вещества (пигмен ...

Получение биогаза
В мировой практике газоснабжения накоплен достаточный опыт использования возобновляемых источников энергии, в том числе энергии биомассы. Наиболее перспективным газообразным топливом являетс ...