Не будет преувеличением утверждение, что уравнение Ван-дер-Ваальса является наиболее известным из всех существующих на данный момент. Оно впервые сформулировано автором в 1873 г. в диссертации “О непрерывности газообразных и жидких состояний” [4].

Математические выражения, относящиеся к уравнению Ван-дер-Ваальса и широко встречающиеся в литературе, приведены ниже.

Стандартный вид уравнения:

; (4.4)

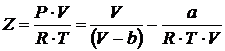. (4.5)

Уравнение в виде полинома:

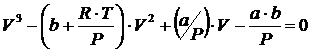; (4.6)

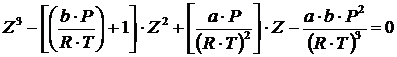. (4.7)

Вириальный вид уравнения:

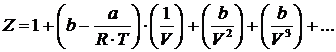(4.8)

Приведенный вид уравнения:

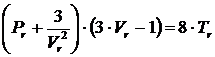, (4.9)

где ; ; .

Параметры, выраженные через критические свойства и полученные из условий (4.2) и (4.3), равны:

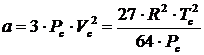; (4.10)

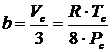, (4.11)

a - параметр, учитывающий действие сил притяжения, b - отталкивания. Последний параметр, называемый эффективным молекулярным объемом, согласно теоретическим расчетам Ван-дер-Ваальса должен в четыре раза превышать действительный объем молекул.

Результаты расчетов, выполненных с использованием уравнения Ван-дер-Ваальса, отличаются невысокой степенью точности и лишь в редких случаях превосходят средний уровень. В этой связи была проделана большая работа в целях усовершенствования данного уравнения путем установления соотношения его параметров с некоторыми другими свойствами помимо параметров критического состояния, а именно с точкой кипения, плотностью, коэффициентом термического расширения и пр. Тем не менее, до настоящего времени из всех известных модификаций уравнения предпочтение отдается его оригинальной редакции. Несмотря на относительную простоту, уравнение Ван-дер-Ваальса позволяет передать сложность взаимоотношений рассматриваемых параметров - давления, температуры, объема. Для иллюстрации сказанного в примере 4.2 избраны три изотермы: одна из них существенно выше критической температуры, вторая близка к ней, а третья проходит через различные области P-V-T пространства - ненасыщенной жидкости, смеси жидкости и пара, область газообразного состояния вещества.

Пример 4.2

Для изобутилбензола с использованием уравнения состояния Ван-дер-Ваальса показать зависимость P от V при 500, 657, 1170 К и объеме 100-3000 см3/ моль. Критические температура и давление равны 650 К и 31 атм соответственно.

Решение

1. Вычислим характеристические константы уравнения:

a = 27·82,062·6502/(64·31) = 3,87·107 (см6·атм)/моль2;

b = 82,06·650/(8·31) = 215 см3/моль.

2. Для заданных температур и дискретных значений молярных объемов вычислим значения давлений. Для 500 К и 1000 см3/моль имеем:

Р = 82,06·500/(1000–215)–3,87·107/10002 = 14 атм.