4. Х5 = 0,7 Хз;

5. Хб = 0,98 Х4;

б ху = 0,02 х4;

7. х8 = 0,05 (х6 + х12);

8. Х9 = 0,95(Х6 + Х12);

э. хю = 0,01 х9;

10. Хц =0,99 Xg;

11. х12 = о,1 (хб + хц);

12. Х13 = 0,9(Х5 + Хц);

13. Х13 = 1000.

Подобную систему уравнений можно довольно легко решить вручную, путем последовательной подстановки, сокращения переменных при вычитании одних уравнений из других и т.д. Однако если число неизвестных очень велико (а в реальных схемах число потоков может достигать многих десятков и даже сотен), возрастает трудоемкость расчетов и вероятность ошибок. В подобных случаях для сокращения числа уравнений можно рекомендовать обозначать неизвестными не количества ценного компонента в каждом из потоков, а суммарные количества, поступающие на операции схемы; при этом, очевидно, число уравнений на 1 больше числа операций. Например, для той же схемы (рис.7) получаем:

1. У1 = G ucx + 0,2 /!, или 0,8 у! = G исх;

2. у2 = 0,8 yi;

3. уз = о, з у2;

4. у4 = 0,98 Уз + 0,1 Уб',

5. у5 = 0,95 у4;

6. у6 = 0,7 у2 + 0,99 у5;

7. G исх = 0,9 у6.

После решения подобной системы уравнений расчет количества ценного компонента в каждом из потоков не вызывает затруднений.

Однако наиболее эффективным способом преодоления трудностей расчета сложных технологических схем является использование компьютеров.

В отличие от человека, выбирающего для каждой конкретной системы уравнений наиболее рациональный путь решения, в программах для цифровых вычислительных машин можно использовать только универсальные, единые для всех систем линейных уравнений способы вычисления. Среди таких способов наиболее распространены метод Гаусса с выбором главного элемента столбца или строки и метод обращения матрицы [2].

До начала вычислений необходимо ввести исходные данные: при использовании метода Гаусса - расширенную матрицу коэффициентов системы линейных уравнений (значения коэффициентов при неизвестных и свободные члены каждого из уравнений):

а при использовании метода обращения матрицы - отдельно квадратную матрицу коэффициентов и вектор-столбец свободных членов:

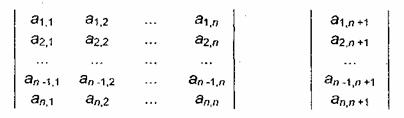
Для составления матрицы коэффициентов члены уравнений, содержащие неизвестные, необходимо расположить слева от знака равенства в порядке возрастания индекса неизвестного, оставив справа только свободные члены; отсутствующие неизвестные вносят в уравнения с коэффициентами, равными нулю. После этого можно приступить к вводу матрицы коэффициентов.

Однако применительно к системе уравнений, получаемой при описании распределения ценного компонента по потокам технологической схемы, этот способ нерационален, так как подавляющая часть коэффициентов равна нулю. Например, при вводе коэффициентов составленной ранее системы из 13 уравнений первые две строки должны быть записаны в следующем виде: - 0,25 Xi + 1 Х2 + О Х3 + О Х4 + О Х5 + О Х6 + О Х7 + О Х8 + О Х9 +

+ о х10 + о хп + ох12+ о х13 = о;

- 0,8 х1 - 0,8 х2 + 1 хЗ + 0 х4 + 0 х5 + 0 хб + 0 х7 + 0 х8 + О Х9 +

+ о Хю+ о х-и +о X-I2 + о х13 = о,

а первые две строки расширенной матрицы коэффициентов соответственно

-0,25 1 000000000000 - 0,8 - 0,8 000000000000

При большом числе неизвестных количество вводимых нулей становится громадным: например, при 40 неизвестных расширенная матрица состоит из 40 х 41 = 1640 коэффициентов, из которых более 1500 будут равны нулю. Очевидно, что ввод подобной матрицы настолько трудоемок и неизбежно сопровождается таким количеством ошибок, что превращается в сложную задачу.

Это затруднение устраняется, если ввод матрицы осуществлять в два этапа: сначала заполнить всю матрицу нулями (эта операция выполняется очень легко), а затем ввести ненулевые коэффициенты, заменяя ими нули.

Ниже описан расчет балансов по ценному компоненту методом Гаусса с помощью программы на языке BASIC и методом обращения матрицы с помощью табличного процессора EXCEL [3, 4].