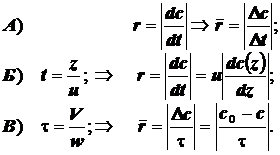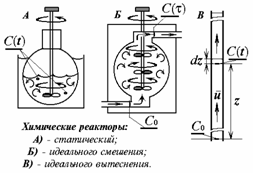
t -время; c0 –стартовая (начальная) концентрация . и c(t) –текущая концентрация реагента;

z- линейное смещение фронта гидродинамического потока (расстояние от стартового сечения);

u- модуль линейной скорости потока в реакторе идеального вытеснения; w- объёмная скорость потока в реакторе идеального смешения ; V- объём реактора идеального смешения; - время контакта в реакторе идеального смешения; r - скорость химической реакции;

Способы математической обработки кинетических данных различают графические и

численные статистические (компьютерные).

Методы определения порядков и констант скоростей химических реакций :

(см. учебник Краснова, стр. 540-541; кафедральный практикум МИТХТ; семнарские занятия)

-графический и статистический подбор оптимальных спрямляющих координат;.

-прямая подстановка в кинетические уравнения и оптимизация постонных (k, n);

-установление взаимосвязи времени полупревращения и начального содержания;

-метод начальных скоростей;

-метод графического дифференцирования (ограниченно и лишь для простых реакций);

-понижение порядка реакции (одно из условий оптимального эксперимента см. выше).

Некоторые полезные сведения о кинетических признаках реакций первого порядка:

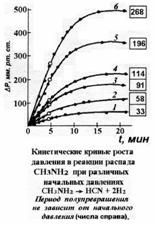
1) Время полупревращения не зависит от начального содержания реагента (парциального

давления или концентрации) (см. рис. на предыдущей странице).

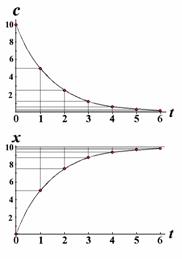
Ещё одно свойство не столь явное, но очень полезное выясняется после некоторых преобразований (рис.). Текущая концентрация реагента равна c=c0×e-kt, а накопившегося продукта x(t)= c0 - c(t)= c0(1- e-kt). (2.13) По окончании реакции получаем

Преобразуем (2.13) к виду e-kt =1- [x(t)/ c0]. (2.14)

Через интервал времени  временная переменная равна уже t+и получается

e-kt+ =1- [x(t+)/ c0] (2.15)

или e-k×e-k t=1- [x(t+)/ c0]. Разделив почленно (2.14) на (2.15), получаем выражения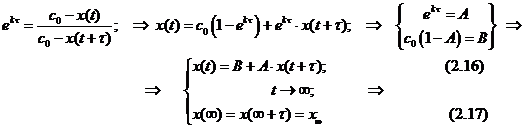

Согласно формуле (2.13) значение x¥ = c0, а согласно (2.17) эта величина лежит на биссектрисе угла между осями декартовых координат (если их масштабы равны) на пересечении с графиком функции (2.16). Так получается один из способов экстраполяционного определения начального содержания реагента. Это особенно важно в тех случаях, когда по каким-то причинам измерить точно эту величину затруднительно. Для этой цели кинетические данные измеряют или представляют через равные интервалы времени. Вся процедура определения x¥ = c0 = a показана ниже на модельном примере.