Молекула состоит из атомов, которые перечислим, нумеруя в любом порядке, но далее всюду соблюдая принятую нумерацию:

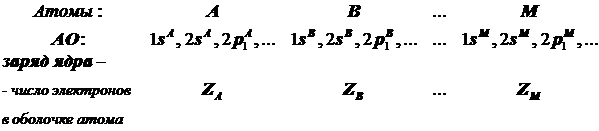
Количество АО у каждого свободного атома не ограничено, и, конечно, наилучшим базисом был бы такой, в котором содержалось максимально возможное количество функций, однако не существует возможности использовать базис бесконечной длины в практических расчётах. Поэтому во всех, даже наиболее совершенных, расчётах используется ограниченное количество базисных функций АО. При выборе базиса используются различные способы ограничения его длины. В более совершенных вариантах теоретических расчётов МО ЛКАО базисные наборы достаточно велики. В более простых приближениях применяют более ограниченные базисные наборы АО. Популярных на тему рисунки татуировок.

Наиболее простым и потому распространённым является валентное приближение. Оно состоит в том, для расчёта электронного строения молекулы используют базис, включающий от каждого атома только АО внешнего оптического слоя. Главное квантовое число всех этих АО одно и то же, но при необходимости базис можно расширить за счёт включения и АО близлежащих подуровней с соседними значениями главного квантового числа. Рассчитываемая часть спектра МО заселяется оптическими электронами, находящимися на внешних валентных АО атомов.

У каждого атома в нейтральном зарядовом состоянии число электронов равно его порядковому номеру в Системе Менделеева. В начале расчёта атомы нумеруются. Все внутренние АО, уровни которых лежат ниже оптических АО, считаются атомными, т.е. их вид считается таким же, как и в свободном атоме, и это недалеко от истины. Набор АО последовательно нумеруется.

Согласно математической схеме квантовой механики по Дираку, всякая волновая функция представляется двумя неразрывно связанными образами-«компонентами»: бра- и кет-векторами Это в чём-то напоминает ситуацию с комплексными числами, каждое из которых само по себе ничего не представляет, обретая смысл лишь в паре со своим комплексно сопряжённым двойником. Похожим образом обстоит дело и с бра-кет- векторами Дирака. Каждый из них неотделим от своего двойника, и лишь вместе они служат основой очень элегантного и компактного построения квантовой механики. Это выглядит следующим образом. Каждой базисной АО отвечают два вектора: бра-вектор и кет-вектор АО, а именно:

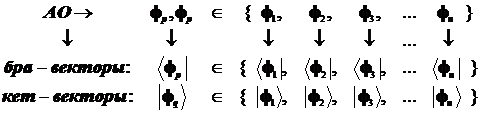
«Бра-кет» - символы это не что иное, как «ско- бки»- символы (от англ. brackets-скобки).

Каждый из этих векторов МО представляется в виде разложения в ряд и при этом:

- бра-векторы МО построены только из бра-векторов АО.

- кет-векторы МО построены только из кет-векторов АО.

В наших расчётах приходится часто иметь дело с массивами однотипных объектов. Условимся опускать многократно повторяющиеся символы. Так, производя вычисления, нет смысла повторять всё время один и тот повто­ряющийся символ в последовательности базисных АО:. С таким же успехом можно ограничиться просто перечислением индексов: 1,2,3, .p, .q, ., в нужном контексте идентифицируя с ними сами АО. В итоге получается предельно компактная запись:

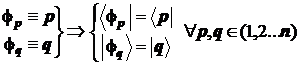Базис:; МО:;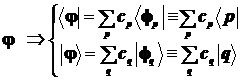

Точно так же, как введены индексные обозначения для базисных АО, ничто не мешает при необходимости ввести индексные обозначения и для МО . Свойства МО и составляющих их БАО следующие:-