1.1.8. Один из уровней замкнутой системы обладает минимально возможной для ее устойчивого существования энергией. Этот уровень называют основным. Обычно с него и начинают нумерацию в порядке возрастания энергии. Остальные уровни, энергия которых больше основного уровня, называют возбужденными.

1.1.9. Если для нумерации уровней пригодны множества N или Zо, то для нумерации состояний иногда их может оказаться недостаточно. У систем, имеющих вырожденные уровни, состояния внутри таких уровней нуждаются в добавочной нумерации. Здесь-то обычно и приходят на помощь фрагменты множества Z или других множеств.

1.1.10. Для каждого из состояний квантово-механической системы вводят свой математический образ и его символ. Такой образ называют волновой функцией, для нее используют символ , либо или какой-либо иной. Совокупность функций состояния называют спектром волновых функций системы и изображают набором – последовательностью:

1.1.11. Каждому состоянию отвечает свой энергетический уровень:

Е1, Е2, Е3,…Еk,….

Множество разрешенных значений энергии образует спектр уровней системы:

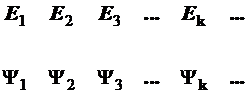
У вырожденных уровней нумерация может быть изменена и дополнена благодаря группировке состояний по уровням.

1.1.12. Введем важные понятия состояний "чистых" и состояний "смешанных". "Чистые" – это дискретные состояния, которые разрешены для частиц, находящихся в стационарных условиях, т.е. не подверженных никаким внешним воздействиям. Такая ситуация идеальна. Реально всякая частица (атом, молекула и т.п.) лишь одна из многих, входящих в термодинамическую систему образца. Последнюю обычно рассматривают в состоянии теплового равновесия, которое в простейшем случае поддерживается за счет соударений, т.е. обмена энергией и состояниями между отдельными частицами. Поэтому приходится ожидать, что всякое реальное состояние квантово-механической системы "смешанное" и включает в себя любое из возможных "чистых" состояний с вероятностью, которая определяется условиями теплового равновесия.

1.1.13. Часто волновую функцию состояния называют вектором состояний. Это связано с особенностями математического аппарата и обусловлено глубокой аналогией, существующей между векторами и волновыми функциями.