Обработка результатов

Для малых выборок использовали распределение Стьюдента, которое связывает между собой ширину доверительного интервала, соответствующую ему вероятность и объем выборочной совокупности.

Для выборки в n результатов рассчитывали среднее

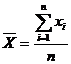
и дисперсию, характеризующую рассеяние результатов относительно среднего

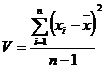
Для характеристики рассеяния результатов в выборочной совокупности использовали также стандартное отклонение

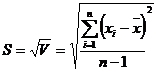
и относительное стандартное отклонение значений

Величину доверительного интервала измеряемой величины для заданной доверительной вероятности рассчитывали, пользуясь выражением

где tpf – коэффициент Стьюдента при заданной вероятности; f=n-1; S – стандартное отклонение измеряемой величины, рассчитанное для выборочной совокупности из n данных. Доверительную вероятность принимали равной 0,95.

Смотрите также

Фосфор и его соединения
Пятая группа Периодической системы включает два типических элемента азот и  фосфор – и подгруппы мышьяка и ванадия. Между первым и вторым типическими  элементами наблюдается значительное раз ...

Мышьяк
Мышьяк (As) Мышьяк (лат. Arsenicum), As, химический элемент V группы периодической системы Менделеева, порядковый номер 33, атомная масса 74,9216; кристаллы серо-стального цвета. Элемент ...

Новые материалы на основе полимерных нанокомпозитов
Сейчас с уверенностью можно утверждать, что одним из наиболее перспективных, а также многообещающих направлений развития современной науки является нанотехнология. Исходя из самого названия ...