Меню сайта
Наши новости
Распространение алкалоидов в растительном мире.
Умягчение воды
Простейшая кинетическая модель активации в ТАКСтатьи и работы по химии / Ионные реакции в растворах. Солевой эффект (в ТАК) / Статьи и работы по химии / Ионные реакции в растворах. Солевой эффект (в ТАК) / Простейшая кинетическая модель активации в ТАК Простейшая кинетическая модель активации в ТАКСтраница 1
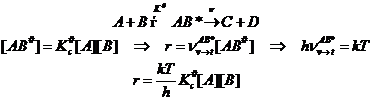 (6.1)
(6.1)
Первая стадия механизма активации бимолекулярная. Она обратимая, на ней образуется активированный комплекс, а он далее распадается по двум маршрутам: а) обратно в реагенты, с которыми он находится в равновесии, и для этого процесса следует ввести константу равновесия, б) в продукты реакции и этот финальный процесс характеризуется некоторой механической частотой распада. Сочетая эти стадии, несложно рассчитать константу скорости реакции. Удобно рассматривать превращение в газовой фазе.
Константа равновесия обратимой стадии может быть выражена следующим способом.
Если стандартные состояния в газовой фазе выбраны согласно обычному термодинамическому правилу, и стандартизованы парциальные давления газообразных участников реакции, то это означает:
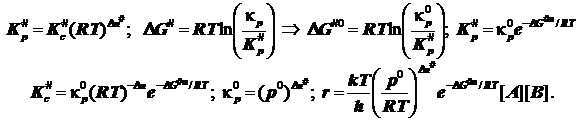
Внимание! Отсюда следует выражение для константы скорости бимолекулярной реакции в ТАК, не вызывающее сомнений в размерности констант скоростей бимолекулярных реакций:
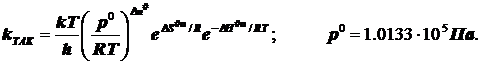 (6.2)
(6.2)
В учебниках чаще всего приводится не столь прозрачное выражение, построенное на иной стандартизации состояний - стандартизуют концентрацию, и в итоге возникает размерность константы скорости, внешне соответствующая моно-, а не би молекулярной реакции. Размерности концентраций оказываются как бы скрыты. У Эйринга, Глесстона и Лейдлера - самих творцов ТАК в книге «Теория абсолютных скоростей реакций» есть анализ, где учтена стандартизация состояний по давлениям. Если стандартным считать состояние с единичными концентрациями реагентов и продуктов, то формулы слегка упростятся, а именно:
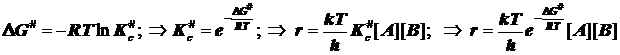 Отсюда следует обычно представленное в учебниках выражение для константы скорости согласно ТАК:
Отсюда следует обычно представленное в учебниках выражение для константы скорости согласно ТАК: ![]() (6.3)
(6.3)
Если не выделить роль стандартного состояния, то теоретическая константа скорости бимолекулярного превращения может обрести чужую размерность, обратную времени, которая будет отвечать мономолекулярной стадии распада активированного комплекса. Активационные величины S#0 и DH#0 нельзя считать обычными термодинамическими функциями состояния. Они не сопоставимы с обычными характеристиками пробега реакции уже потому, что методов их прямого термохимического измерения просто не существует . По этой причине их можно назвать квазитермодинамическими характеристиками процесса активации.
При образовании частицы активированного комплекса из двух исходных частиц имеет место ![]() , и в результате получается
, и в результате получается
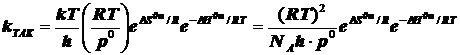 (6.4)
(6.4)
Размерность константы скорости обычная для реакции второго порядка:
![]()
Эмпирическая энергия активации по Аррениусу и её сравнение с близкими аналогичными активационными параметрами (энергиями) ТАС и ТАК:
Основа - уравнение Аррениуса в дифференциальной форме: ![]()
1) в ТАС получаем:
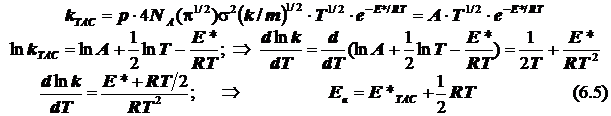
2.1) ТАК. Случай 1. (Общий подход при условии стандартизации концентраций)
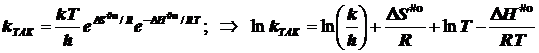
подстановка в уравнение Аррениуса даёт
![]()
2.2) ТАК. Случай 2. (Частный случай бимолекулярной стадии активации
![]() )
)
Энергия активации по Аррениусу для бимолекулярной реакции:
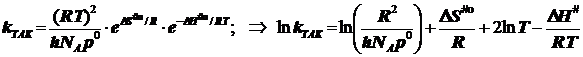
Внимание!!! Полагаем чаще всего ![]()
2.2) Исходя из стандартизации давления, получаем энергию активации:
![]()
![]()
![]() (6.7)
(6.7)
2.3) Это же получается для бимолекулярной реакции и при стандартизации концентрации:
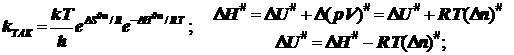 (6.8)
(6.8)
![]()
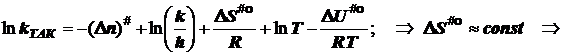
Смотрите также
Концептуальные уровни в познании веществ и химические системы
В данной работе рассматривается тема
"Концептуальные уровни в познании веществ и химические системы".
Химию обычно рассматривали как науку о составе и качественном превращении
раз ...
О-хлорстирол
...
Физико-химические свойства йода и его соединений
Йод
открыт французским химиком Куртуа в 1811 году, он относится к VII группе
периодической системы Д.И. Менделеева. Порядковый номер элемента - 53. В
природе он находится в виде стабильного ...


